A transverse sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string with a speed of 100 cm/s. Take the origin at left end of the string. At time t = 0 the left end of the string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system )
y=10sin(0.01π×−πt)
y=10sin(πt−0.01π×)
y=10sin(0.02π×−0.01πt)
y=10sin(πt−0.02π×)
The correct Answer is:A
To find the equation of the transverse sine wave, we can follow these steps:
Step 1: Identify the given parameters
- Amplitude A=10 cm
- Wavelength λ=200 cm
- Speed of the wave v=100 cm/s
Step 2: Write the general form of the wave equation
The general form of a transverse wave traveling in the positive x-direction is given by:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
Step 3: Calculate the wave number k
The wave number k is given by the formula:
k=2πλ
Substituting the value of λ:
k=2π200=π100 cm−1
Step 4: Calculate the frequency f
The frequency f can be calculated using the formula:
f=vλ
Substituting the values of v and λ:
f=100200=0.5 Hz
Step 5: Calculate the angular frequency ω
The angular frequency ω is given by:
ω=2πf
Substituting the value of f:
ω=2π×0.5=π rad/s
Step 6: Write the wave equation
Now we can substitute the values of A, k, and ω into the wave equation:
y(x,t)=10sin(π100x−πt)
Step 7: Consider the initial condition
At t=0, the left end of the string (at x=0) is moving downward. Since the sine function starts at zero, we need to adjust the equation to reflect that the wave is moving downward at the origin. The downward motion indicates that we should use:
y(x,t)=10sin(π100x−πt+π2)
This is equivalent to:
y(x,t)=10cos(π100x−πt)
Thus, the final equation of the wave is:
y(x,t)=10cos(π100x−πt) cm
Final Answer
The equation of the wave is:
y(x,t)=10cos(π100x−πt) cm
---
- Amplitude A=10 cm
- Wavelength λ=200 cm
- Speed of the wave v=100 cm/s
The general form of a transverse wave traveling in the positive x-direction is given by:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
The wave number k is given by the formula:
k=2πλ
Substituting the value of λ:
k=2π200=π100 cm−1
The frequency f can be calculated using the formula:
f=vλ
Substituting the values of v and λ:
f=100200=0.5 Hz
The angular frequency ω is given by:
ω=2πf
Substituting the value of f:
ω=2π×0.5=π rad/s
Now we can substitute the values of A, k, and ω into the wave equation:
y(x,t)=10sin(π100x−πt)
At t=0, the left end of the string (at x=0) is moving downward. Since the sine function starts at zero, we need to adjust the equation to reflect that the wave is moving downward at the origin. The downward motion indicates that we should use:
y(x,t)=10sin(π100x−πt+π2)
This is equivalent to:
y(x,t)=10cos(π100x−πt)
Thus, the final equation of the wave is:
y(x,t)=10cos(π100x−πt) cm
The equation of the wave is:
y(x,t)=10cos(π100x−πt) cm
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions

System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View SolutionA transverse sinusoidal wave of amplitude a, wavelength λ and frequency f is travelling on a stretched string. The maximum speed of any point in the string is v/10, where v is the speed of propagation of the wave. If a=10−3m and v=10ms−1, then λ and f are given by
View SolutionTwo sinusoidal waves with same wavelengths and amplitudes travel in opposite directions along a string with a speed 10ms−1. If the minimum time interval between two instant when the string is flat is 0.5s, the wavelength of the waves is
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
View SolutionA transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
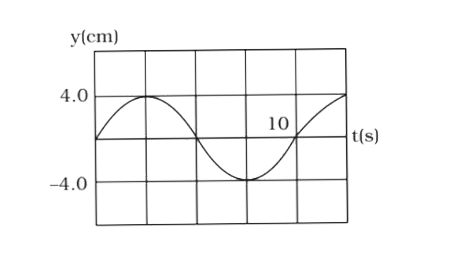
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?
View SolutionSmall amplitude progressive wave in a stretched string has a speed of 100cm/s.and frequency 100 Hz. The phase difference between two points 2.75 cm apart on the string in radians, is
View SolutionA transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View Solution