Question

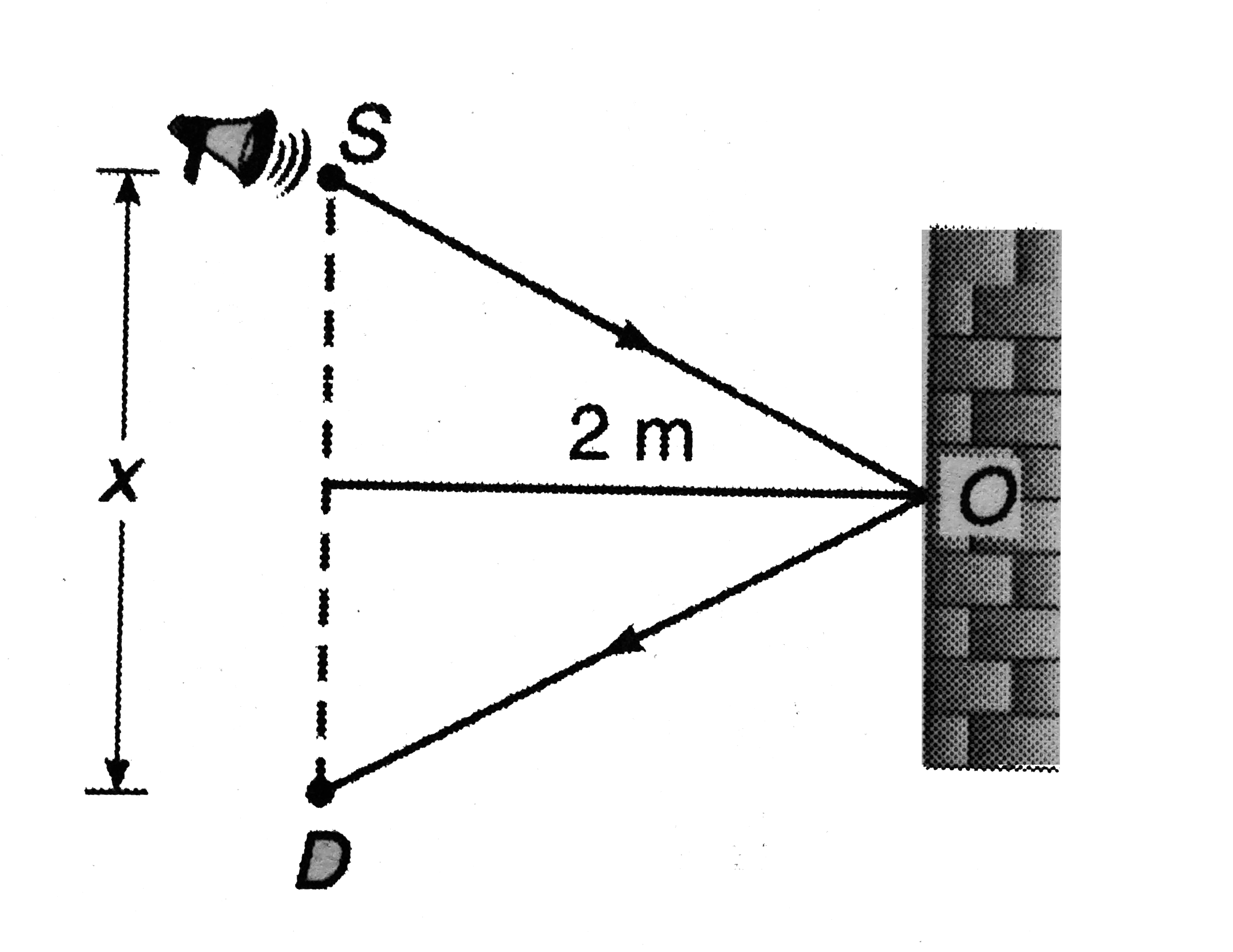
A soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s

Options

A. 4m
B. 3 m
C. 1 m
D. 2m

Answer

B

Explanation

To solve the problem step by step, we need to find the minimum distance between the source and the detector for which maximum sound is recorded at the detector.

Step 1: Understand the Setup
We have a sound source emitting sound waves with a frequency of 165 Hz, placed 2 m away from a wall. A detector is also placed 2 m away from the wall, directly in line with the source.

Step 2: Calculate the Wavelength
The speed of sound is given as 330 m/s. We can calculate the wavelength (λ) using the formula:
\( \lambda = \frac{v}{f} \)
where \( v \) is the speed of sound and \( f \) is the frequency.

Substituting the values:
\( \lambda = \frac{330 \, \text{m/s}}{165 \, \text{Hz}} = 2 \, \text{m} \)

Step 3: Determine the Path Difference for Maximum Sound
For maximum sound to be recorded at the detector, the path difference (Δx) between the sound waves reaching the detector directly and the sound waves reflecting off the wall must be equal to an integer multiple of the wavelength:
\( \Delta x = n\lambda \)
For the first maximum, we take \( n = 1 \):
\( \Delta x = \lambda = 2 \, \text{m} \)

Step 4: Set Up the Geometry
Let \( d \) be the distance from the source to the wall (which is given as 2 m) and \( x \) be the distance from the source to the detector. The sound travels directly to the detector and also reflects off the wall.

The total distance traveled by the sound reflecting off the wall is:
\( \text{Distance}_{\text{reflected}} = d + d = 2d \)
The distance traveled directly to the detector is:
\( \text{Distance}_{\text{direct}} = x \)

Step 5: Write the Path Difference Equation
The path difference can be expressed as:
\( \Delta x = 2d - x \)
Setting this equal to the wavelength for maximum sound:
\( 2d - x = 2 \)

Step 6: Substitute the Known Distance
Since \( d = 2 \, \text{m} \):
\( 2(2) - x = 2 \)
\( 4 - x = 2 \)
\( x = 2 \, \text{m} \)

Step 7: Calculate the Minimum Distance Between Source and Detector
The total distance between the source and the detector is:
\( \text{Distance}_{\text{total}} = d + x = 2 + 2 = 4 \, \text{m} \)

Final Answer
The minimum distance between the source and the detector for which maximum sound is recorded is 4 meters.

---