Question

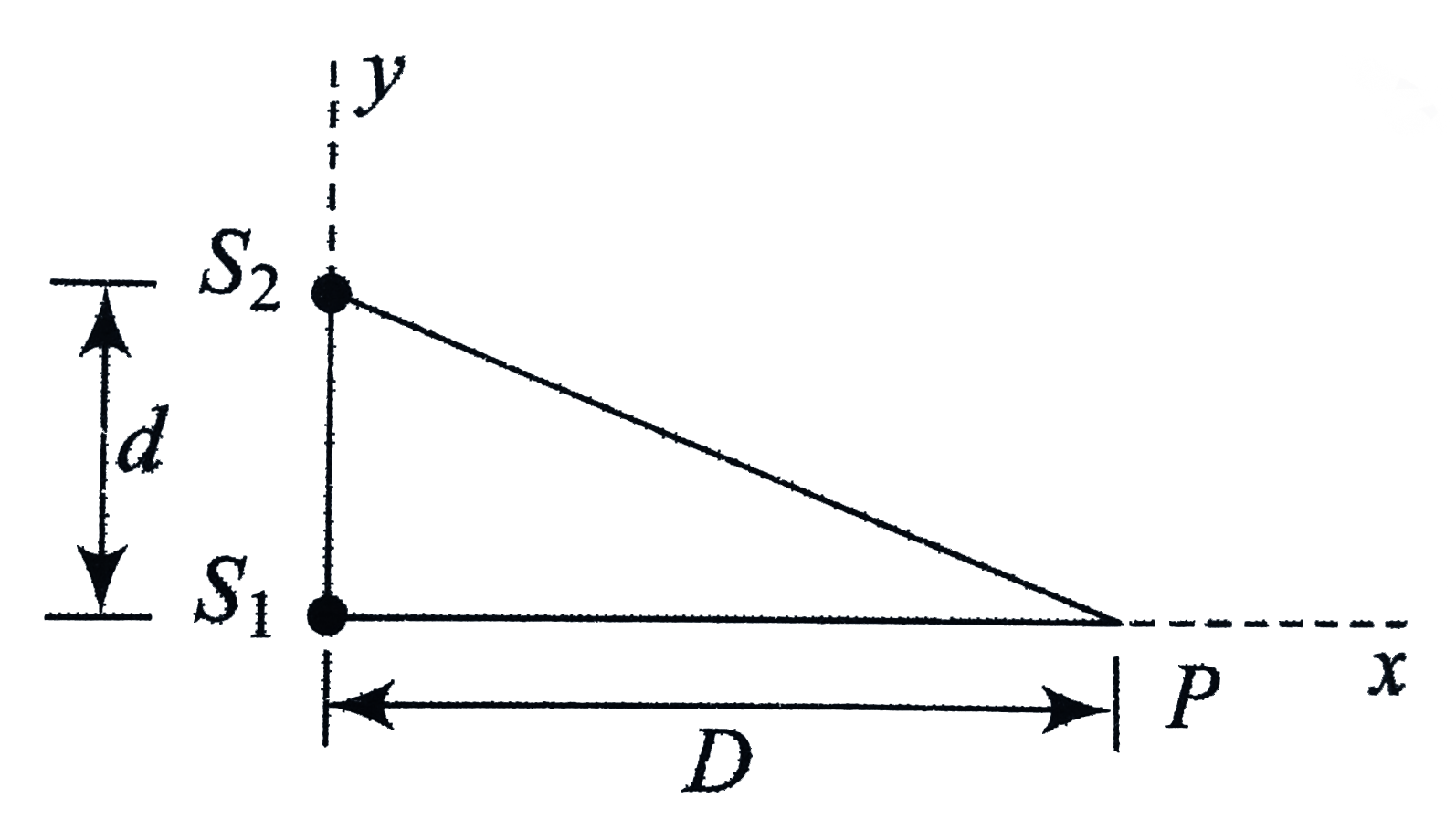
Two source of sound, $S_1$ and $S_2$, emitting waves of equal wavelength $2cm$, are placed with a separation of $3cm$ between them. A detector can be moved on a line parallel to $S_1{S}_2$ and at a distance $24cm$ from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.

Explanation

To solve the problem step by step, we need to analyze the situation involving two sound sources and the detector's position. Here’s how we can approach it:

Step 1: Understand the Setup
We have two sound sources, \( S_1 \) and \( S_2 \), separated by a distance of \( 3 \, \text{cm} \). The wavelength of the sound waves emitted by both sources is \( 2 \, \text{cm} \). The detector is initially positioned equidistant from both sources at a distance of \( 24 \, \text{cm} \) away from the line connecting the sources.

Step 2: Determine the Initial Position of the Detector
Since the detector is equidistant from both sources, we can denote the distance from the line connecting the sources to the detector as \( d = 24 \, \text{cm} \). The horizontal distance from \( S_1 \) to the detector can be calculated using the right triangle formed by the sources and the detector.

Step 3: Calculate the Path Difference
The path difference \( \Delta d \) between the waves reaching the detector from \( S_1 \) and \( S_2 \) can be expressed as:
\( \Delta d = d_2 - d_1 \)
where \( d_1 \) and \( d_2 \) are the distances from the detector to \( S_1 \) and \( S_2 \) respectively.

Step 4: Condition for Minimum Sound
For destructive interference (minimum sound), the path difference must be equal to an odd multiple of half the wavelength:
\( \Delta d = \left( n + \frac{1}{2} \right) \lambda \)
where \( n \) is an integer. For the first minimum, we can set \( n = 0 \), thus:
\( \Delta d = \frac{\lambda}{2} = \frac{2 \, \text{cm}}{2} = 1 \, \text{cm} \)

Step 5: Set Up the Equation
We can express the path difference in terms of the horizontal shift \( x \) of the detector:
\( \Delta d = \sqrt{(24^2 + (1.5 + x)^2)} - \sqrt{(24^2 + (1.5 - x)^2)} \)
Setting this equal to \( 1 \, \text{cm} \) gives us the equation to solve for \( x \).

Step 6: Solve the Equation
Squaring both sides and simplifying will lead to a quadratic equation in \( x \). After solving, we find that:
\( x = 12 \, \text{cm} \)
This means the detector must be shifted \( 12 \, \text{cm} \) to detect the minimum sound.

Final Answer
The minimum distance through which the detector should be shifted to detect a minimum of sound is \( 12 \, \text{cm} \).

---