Velocity of secnod in air is 320 m/s. Neglecting end correctionss, the air column in the pipe can resonate for sound of frequency
80 Hz
240 Hz
320 Hz
400 Hz
The correct Answer is:A, B, D
To solve the problem of finding the resonant frequencies of an air column in a closed pipe, we can follow these steps:
1. Understand the Problem: We know the speed of sound in air (V) is 320 m/s. We need to determine the resonant frequencies of the air column in a closed organ pipe.
2. Identify the Fundamental Frequency: For a closed organ pipe, the fundamental frequency (first harmonic) occurs when there is one node at the closed end and one antinode at the open end. The length of the pipe (L) is equal to one quarter of the wavelength (λ) of the sound wave:
L=λ4
3. Express Wavelength in Terms of Length: Rearranging the equation gives:
λ=4L
4. Use the Frequency-Wavelength Relationship: The frequency (f) of a wave is related to its speed and wavelength by the equation:
f=Vλ
Substituting the expression for λ from the previous step:
f=V4L
5. Calculate the Fundamental Frequency: If we assume the length of the pipe (L) is 1 meter (as an example), we can calculate the fundamental frequency:
f1=320m/s4×1m=3204=80Hz
6. Identify Higher Harmonics: The frequencies of the higher harmonics (odd harmonics) can be expressed as:
fn=(2n+1)V4L
where n=0,1,2,…
7. Calculate the First Few Frequencies:
- For n=0:
f1=80Hz
- For n=1:
f3=3×3204×1=9604=240Hz
- For n=2:
f5=5×3204×1=16004=400Hz
8. Conclusion: The resonant frequencies of the air column in the pipe are 80 Hz, 240 Hz, and 400 Hz, corresponding to the first, third, and fifth harmonics, respectively.
L=λ4
λ=4L
f=Vλ
Substituting the expression for λ from the previous step:
f=V4L
f1=320m/s4×1m=3204=80Hz
fn=(2n+1)V4L
where n=0,1,2,…
- For n=0:
f1=80Hz
- For n=1:
f3=3×3204×1=9604=240Hz
- For n=2:
f5=5×3204×1=16004=400Hz
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT
62 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A narrow pipe of length 2m is closed at one end. The velocity of sound in air is 320 m/s. Neglecting end corrections , the air column in the pipe will resonate for sound of frequencies :
View SolutionSpeed of sound in air is 320m/s . A pipe closed at one end has a length of 1m and there is another pipe open at both ends having a length of 1.6m . Neglecting end corrections, both the air columns in the pipes can resonate for sound of frequency
View Solution
Knowledge Check
velocity of sound in air is 320 m/s. A pipe closed at one end has a length of 1 m. Neglecting end corrections, the air column in the pipe can resonates for sound of frequency
A80 HzB240 HzC320 HzD400 Hz
A pipe 1 m length is closed at one end. Taking the speed of sound in air as 320ms−1 .the air column in the pipe cannot resonate for the frequency (in Hz )
View SolutionThe velocity of sound in air is 340ms−1. A pipe closed at one end has a length of 170 cm. neglecting the end correction, the frquencies at which the pipe can resonate are
View SolutionVelocity of sound in air is 320m/s. The resonant pipe shown in Fig. 7.81 cannot vibrate with a sound of frequency .

View SolutionVelocity of sound in air is 320 m/s. For an organ pipe closed at one end of length 2 m the resonating frequency may be
View SolutionIn each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.
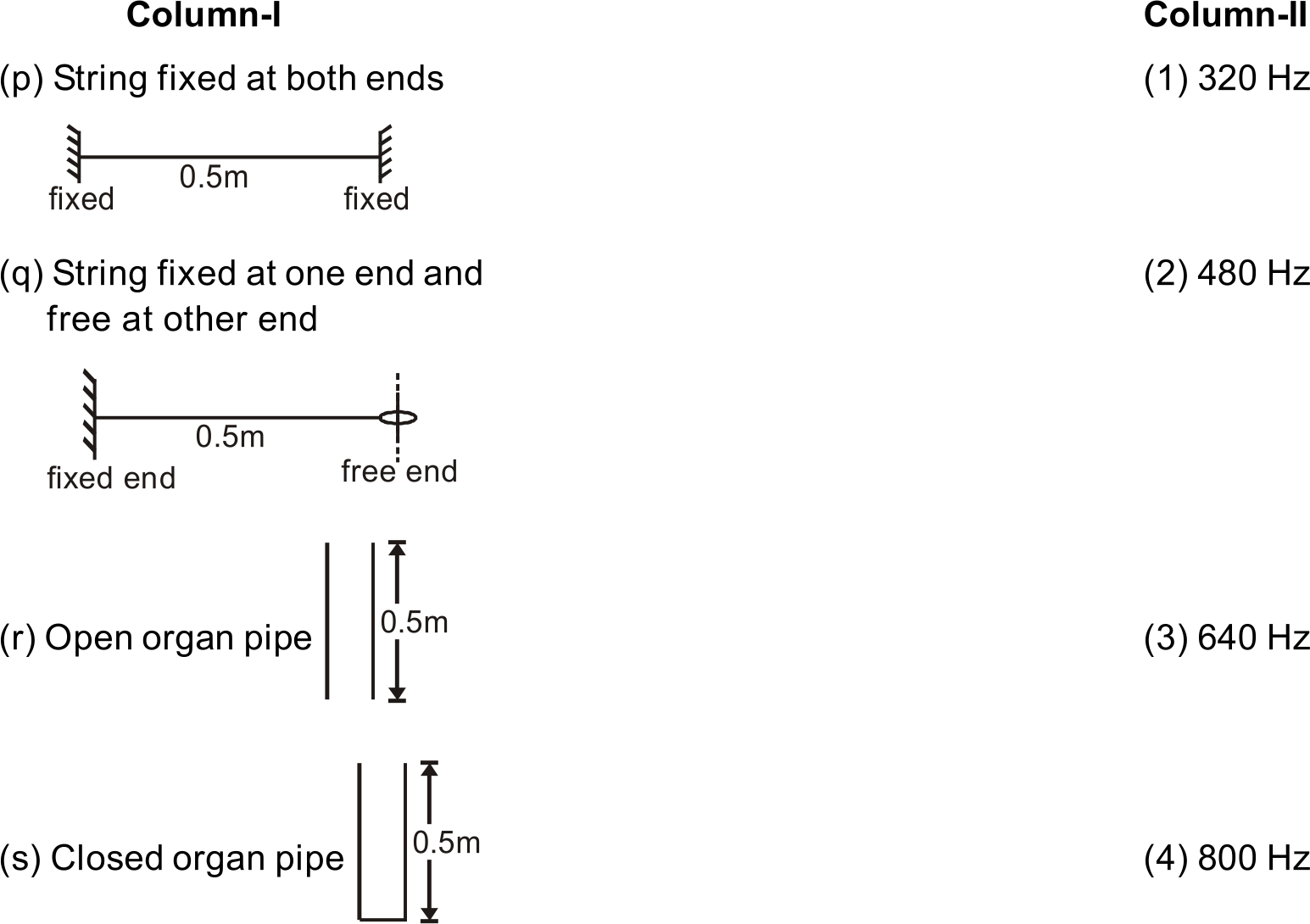
View SolutionAn organ pipe closed at one end has a length 1m and an open organ pipe has a length 1.6 m . The speed of sound in air is 320 m/s . The two pipes can resonates for a sound of frequency
View SolutionIf the velocity of sound in air is 320m/s, then the maximum and minimum length of a pipe closed at one end , that would produce a just audible sound would be
View Solution
