Two identical thin planoconvex lenses of refractive index n are silvered, one on the plane side and other on the convex side. The ratio of their for lengths is
n/(n−1)
(n−1)/n
(n+1)/n
n
The correct Answer is:A
To solve the problem of finding the ratio of the focal lengths of two identical thin planoconvex lenses that are silvered on different sides, we will follow these steps:
Step 1: Understand the Configuration
We have two identical planoconvex lenses:
- Lens 1: Silvered on the plane side.
- Lens 2: Silvered on the convex side.
Step 2: Focal Length of Lens 1 (Silvered on the Plane Side)
For Lens 1, when the plane side is silvered, it behaves like a concave mirror. The focal length f1 of a concave mirror is given by:
f1=−R2
where R is the radius of curvature of the convex surface of the lens.
Step 3: Focal Length of Lens 2 (Silvered on the Convex Side)
For Lens 2, when the convex side is silvered, it behaves like a concave lens. The focal length f2 of a planoconvex lens is given by:
1f2=(n−1)(1R−1∞)=n−1R
Thus, the focal length f2 is:
f2=Rn−1
Step 4: Calculate the Ratio of Focal Lengths
Now, we need to find the ratio of the focal lengths f1f2:
f1f2=−R2Rn−1=−R2⋅n−1R=−n−12
Since we are interested in the absolute ratio, we can ignore the negative sign:
f1f2=n−12
Step 5: Final Result
Thus, the ratio of the focal lengths of the two lenses is:
f1f2=nn−1
Conclusion
The final answer is:
Ratio of focal lengths =nn−1
We have two identical planoconvex lenses:
- Lens 1: Silvered on the plane side.
- Lens 2: Silvered on the convex side.
For Lens 1, when the plane side is silvered, it behaves like a concave mirror. The focal length f1 of a concave mirror is given by:
f1=−R2
where R is the radius of curvature of the convex surface of the lens.
For Lens 2, when the convex side is silvered, it behaves like a concave lens. The focal length f2 of a planoconvex lens is given by:
1f2=(n−1)(1R−1∞)=n−1R
Thus, the focal length f2 is:
f2=Rn−1
Now, we need to find the ratio of the focal lengths f1f2:
f1f2=−R2Rn−1=−R2⋅n−1R=−n−12
Since we are interested in the absolute ratio, we can ignore the negative sign:
f1f2=n−12
Thus, the ratio of the focal lengths of the two lenses is:
f1f2=nn−1
The final answer is:
Ratio of focal lengths =nn−1
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
Two identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
View SolutionTwo identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20 cm are placed with their convex sufaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7 The focal length of the combination is
View SolutionTwo similar planoconvex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

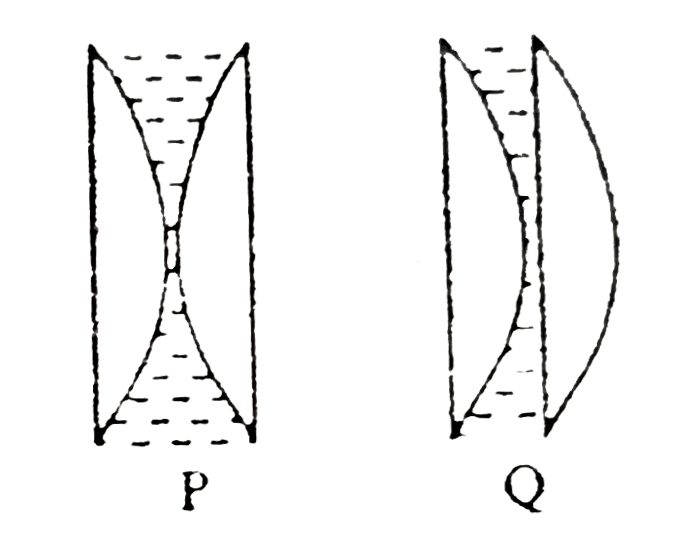
View SolutionA liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown. The system is
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View SolutionTwo glasses with refractive indices of 1.5and1.7 are used to make two indentical double convex lenses.
Find the ratio between their focal lengths.
How will each of these lenses act on a ray parallel to its optical axis if the lenses are submerged into a transparent liquid with a refractive index of 1.6?
View SolutionA thin plano - convex lens acts like a concave mirror of focal length 0.2 m, when silvered on its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the lens will be
View SolutionThe plane surface of a plano-convex lens of refracting index 1.5, is silvered. The radius of curvature of curved surface is R. Find the focal length of the mirror thus formed.
View SolutionTwo identical equi- concave lenses made of glass of refractive index 1.5 placed in contact has power P. When a liquid of refractive index μ is filled in the gap between the concave lenses,the power becomes (P3).The value of μ is R2.Find K.
View Solution
