A liquid of refractive index $1.33$ is placed between two identical plano-convex lenses, with refractive index $1.50$ . Two possible arrangement $P$ and $Q$ are shown. The system is
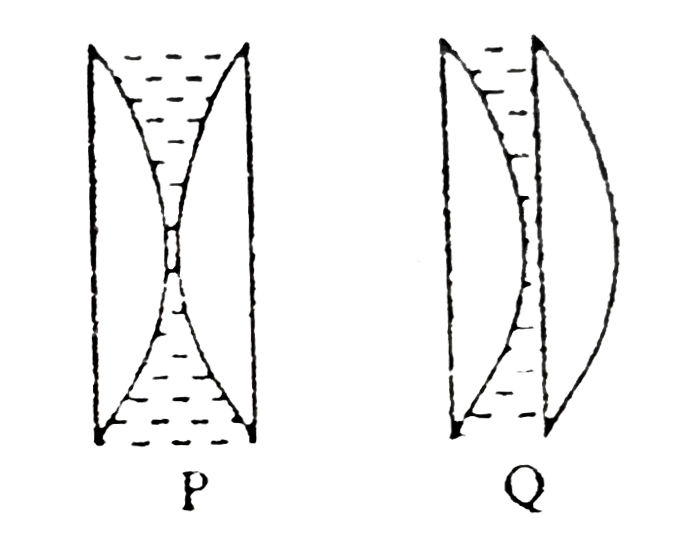
$A liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown. The system is$

divergent in $P$ , convergent in $Q$

convergent in $P$ , divergent in $Q$

convergent in both.

divergent in both.

Video Solution

Text Solution

Verified by Experts

$\frac{1}{f_{1}} = \frac{(1.5 - 1)}{R} + (\frac{4}{3} - 1) (- \frac{1}{R} - \frac{1}{R}) + (\frac{1.5 - 1}{R}) = \frac{1}{R} - \frac{2}{3 R} = \frac{1}{3 R}$
$\frac{1}{f_{2}} = \frac{(1.5 - 1)}{R} + (\frac{4}{3} - 1) (- \frac{1}{R}) + (\frac{1.5 - 1}{R}) = \frac{1}{R} - \frac{1}{3 R} = \frac{2}{3 R}$
$\Rightarrow$ Convergent in both.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View Solution
Two identical thin planoconvex lenses of refractive index n are silvered, one on the plane side and other on the convex side. The ratio of their for lengths is
View Solution
A double convex lens of refractive index $m_{1}$ is immersed in a liquid of refractive index $m_{2}$ . This lens will act as:
View Solution
The adjacent figure shows a thin plano-convex lens of refractive index $μ_{1}$ and a thin plano-concave lens of refractive index $μ_{2}$ , both having same radius of curvature R of their curved surfaces. The thin lens of refractive index $μ_{3}$ has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View Solution
A prism of refractive index $1.53$ is placed in water of refractive index $1.33$ . If the angle of prism is $60^{\circ}$ , calculate the angle of minimum deviation in water.
View Solution
A plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View Solution
A liquid of refractive index 1.6 is contained in the cavity of a glass specimen of refractive index 1.5 as shown in figure. If each of the curve surface has a radius of curvature of 0.20m, the arrangement obehaves as a

View Solution
A lens is made of flint glass (refractive index $= 1.5$ ). When the lens is immersed in a liquid of refractive index $1.25$ , the focal length:
View Solution
Focal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View Solution
A glass lens of refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to mark the lens disappear?
View Solution

A liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown. The system is

1f1=(1.5−1)R+(43−1)(−1R−1R)+(1.5−1R)=1R−23R=13R 1f2=(1.5−1)R+(43−1)(−1R)+(1.5−1R)=1R−13R=23R ⇒ Convergent in both.

Similar Questions

Recommended Questions