A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What is the value of x (in cm ) so that images from by both the lenses coincides ?
20(√3−1) and 1√3
10(√3−1)
20√3
none of these
The correct Answer is:D
To solve the problem, we need to find the distance x from the convex lens such that the images formed by both the convex lens and the concave lens coincide.
1. Identify the Lenses and Their Focal Lengths:
- Convex lens (Focal length, f1=+20 cm)
- Concave lens (Focal length, f2=−10 cm)
- Distance between the two lenses = 20 cm
2. Set Up the Object and Image Distances:
- Let the object be placed at a distance x from the convex lens.
- Therefore, the distance of the object from the concave lens will be 20−x cm.
3. Apply the Lens Formula for the Convex Lens:
The lens formula is given by:
1f=1v−1u
For the convex lens:
1f1=1v1−1u1
Here, u1=−x (object distance is taken as negative for real objects) and f1=20 cm.
Thus, we have:
120=1v1+1x
Rearranging gives:
1v1=120−1x(1)
4. Apply the Lens Formula for the Concave Lens:
For the concave lens:
1f2=1v2−1u2
Here, u2=−(20−x) and f2=−10 cm.
Thus, we have:
−110=1v2+1(20−x)
Rearranging gives:
1v2=−110−1(20−x)(2)
5. Set the Images to Coincide:
Since the images coincide, we set v1=v2:
120−1x=−110−1(20−x)
6. Solve for x:
Cross-multiplying and simplifying the equation leads to:
120+110=1x−1(20−x)
This can be solved to find x.
After performing the algebra, we find:
x=211+√3≈21 cm
Final Answer:
The value of x is 211+√3 cm.
- Convex lens (Focal length, f1=+20 cm)
- Concave lens (Focal length, f2=−10 cm)
- Distance between the two lenses = 20 cm
- Let the object be placed at a distance x from the convex lens.
- Therefore, the distance of the object from the concave lens will be 20−x cm.
The lens formula is given by:
1f=1v−1u
For the convex lens:
1f1=1v1−1u1
Here, u1=−x (object distance is taken as negative for real objects) and f1=20 cm.
Thus, we have:
120=1v1+1x
Rearranging gives:
1v1=120−1x(1)
For the concave lens:
1f2=1v2−1u2
Here, u2=−(20−x) and f2=−10 cm.
Thus, we have:
−110=1v2+1(20−x)
Rearranging gives:
1v2=−110−1(20−x)(2)
Since the images coincide, we set v1=v2:
120−1x=−110−1(20−x)
Cross-multiplying and simplifying the equation leads to:
120+110=1x−1(20−x)
This can be solved to find x.
x=211+√3≈21 cm
The value of x is 211+√3 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Matrix matching type Q.
8 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What will be the linear magnification produced convex lens and concave lens individually ?
View SolutionA convex lens of focal length 80 cm and a concave lens of focal length 50 cm are combined toghether. What will be their resulting power ?
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png)
View SolutionA convex lens of focal length 20cm and a concave lens of focal length f are mounted coaxially 5cm apart. Parallel beam of light incident on the convex lens emerges from the concave lens as a parallel beam. Then, f in cm is
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
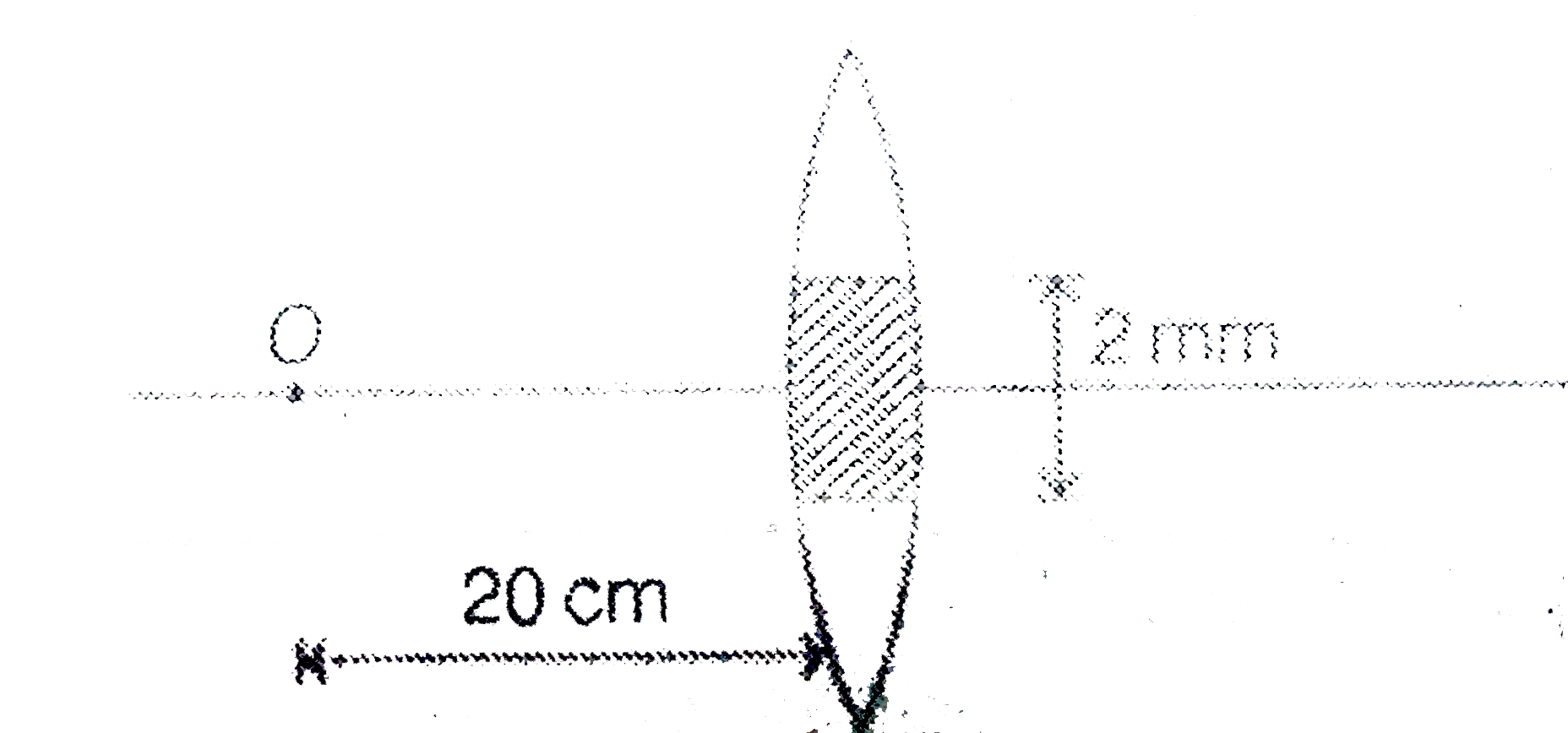
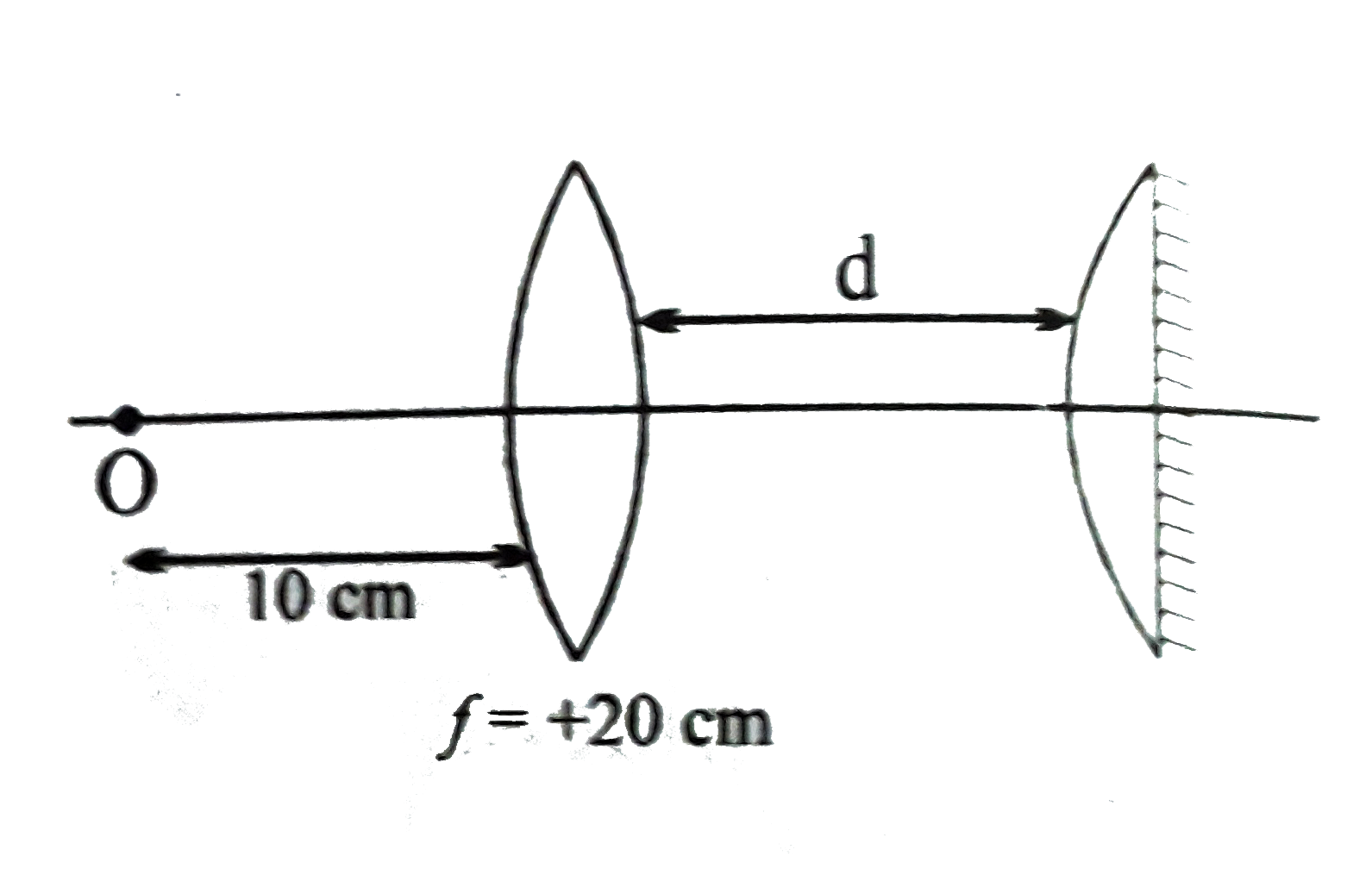
View SolutionA convex lens of focal length 20cm and another plano convex lens of focal length 40cm are placed co-axially . The plano convex lens is silvered on plane surface. What should be the distance (in cm) so that final image of the object 'O' is formed on O itself.
View Solution
