Three capacitors 2μF, 3μF and 5μF can withstand voltages to 3V,2V and 1V respectively. Their series combination can withstand a maximum voltage equal to
5 V
31/6 V
26/5 V
6 V
The correct Answer is:B
To solve the problem of finding the maximum voltage that can be withstood by the series combination of three capacitors (2 µF, 3 µF, and 5 µF), we will follow these steps:
Step 1: Determine the maximum charge for each capacitor
We start by calculating the maximum charge that each capacitor can store based on their capacitance and the maximum voltage they can withstand.
1. For the 2 µF capacitor:
Q1=C1×V1=2μF×3V=6μC
2. For the 3 µF capacitor:
Q2=C2×V2=3μF×2V=6μC
3. For the 5 µF capacitor:
Q3=C3×V3=5μF×1V=5μC
Step 2: Identify the limiting charge
In a series combination of capacitors, the charge stored on each capacitor is the same. Therefore, the maximum charge that can be stored in the series combination is determined by the capacitor with the smallest maximum charge.
The maximum charges calculated are:
- Q1=6μC
- Q2=6μC
- Q3=5μC
Thus, the limiting charge Qmax is:
Qmax=min(Q1,Q2,Q3)=5μC
Step 3: Calculate the equivalent capacitance
Next, we calculate the equivalent capacitance Ceq of the series combination using the formula:
1Ceq=1C1+1C2+1C3
Substituting the values:
1Ceq=12μF+13μF+15μF
Finding a common denominator (which is 30):
1Ceq=1530+1030+630=3130
Thus,
Ceq=3031μF
Step 4: Calculate the maximum voltage across the series combination
Using the relationship between charge, capacitance, and voltage:
Q=Ceq×Vmax
We can rearrange this to find Vmax:
Vmax=QmaxCeq
Substituting the known values:
Vmax=5μC3031μF=5×3130V=15530V=316V
Conclusion
The maximum voltage that can be withstood by the series combination of the three capacitors is:
Vmax=316V≈5.17V
We start by calculating the maximum charge that each capacitor can store based on their capacitance and the maximum voltage they can withstand.
Q1=C1×V1=2μF×3V=6μC
Q2=C2×V2=3μF×2V=6μC
Q3=C3×V3=5μF×1V=5μC
In a series combination of capacitors, the charge stored on each capacitor is the same. Therefore, the maximum charge that can be stored in the series combination is determined by the capacitor with the smallest maximum charge.
- Q1=6μC
- Q2=6μC
- Q3=5μC
Qmax=min(Q1,Q2,Q3)=5μC
Next, we calculate the equivalent capacitance Ceq of the series combination using the formula:
1Ceq=1C1+1C2+1C3
Substituting the values:
1Ceq=12μF+13μF+15μF
Finding a common denominator (which is 30):
1Ceq=1530+1030+630=3130
Thus,
Ceq=3031μF
Using the relationship between charge, capacitance, and voltage:
Q=Ceq×Vmax
We can rearrange this to find Vmax:
Vmax=QmaxCeq
Substituting the known values:
Vmax=5μC3031μF=5×3130V=15530V=316V
The maximum voltage that can be withstood by the series combination of the three capacitors is:
Vmax=316V≈5.17V
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Three capacitors 2μF,3μFand6μF are joined with each other. What is the minimum effective capacitance?
View Solution
Three capacitors of capacitances 5μF,2μF and 2μF are charged to 20 V, 30 V and 10 V respectively and then connected in the circuit with polarities as shown. The magnitude of charge flown through the battery after closing the switch S is
View SolutionThree capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.
View SolutionA capacitor of capacitance C1=1μF withstand a maximum voltage of V1=6KV, and another capacitor of capacitance C2=2μF, can with stand a maximum voltage of V2=4KV. If they are connected in series, what maximum voltage will the system withstand?
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
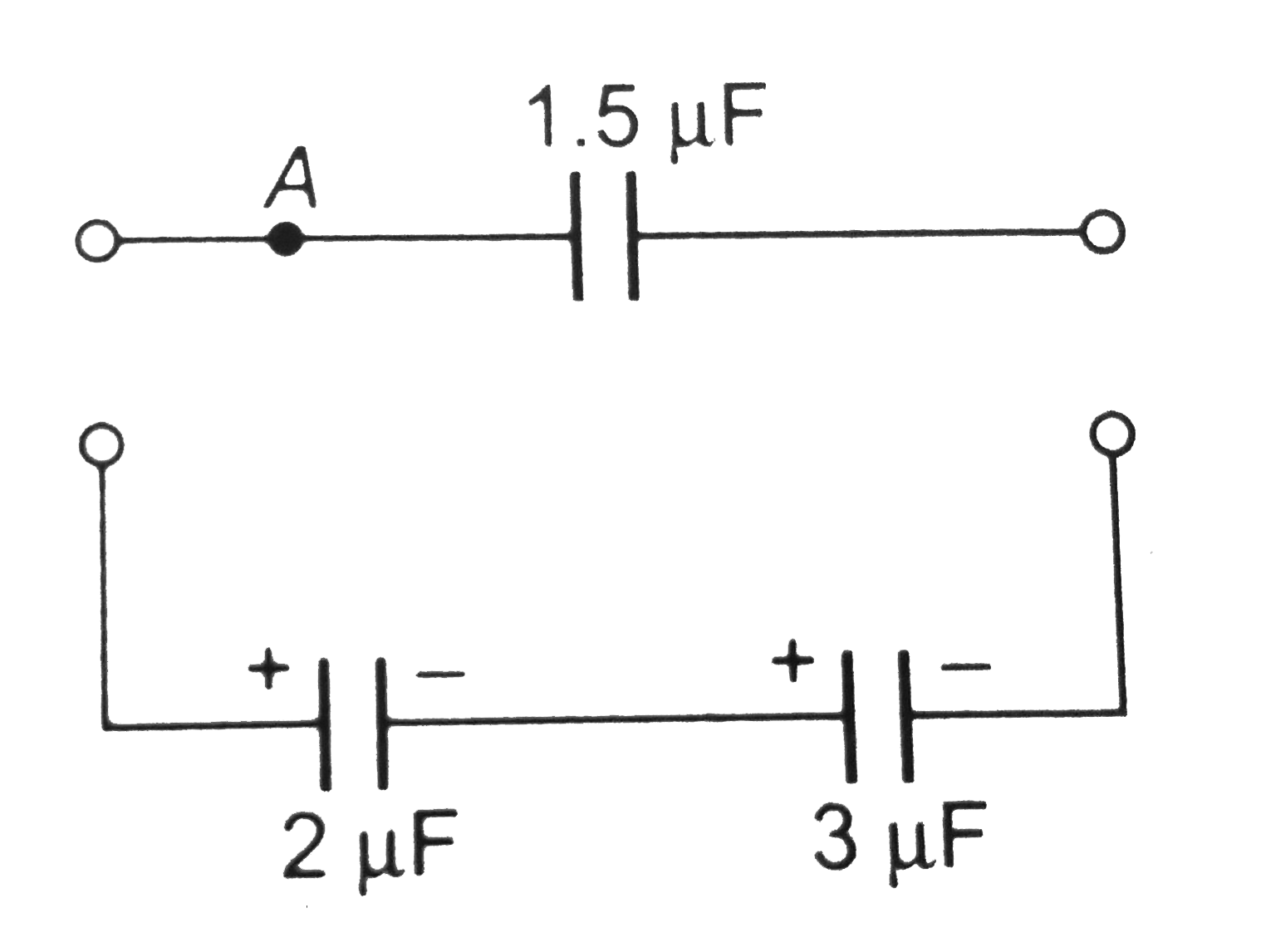
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

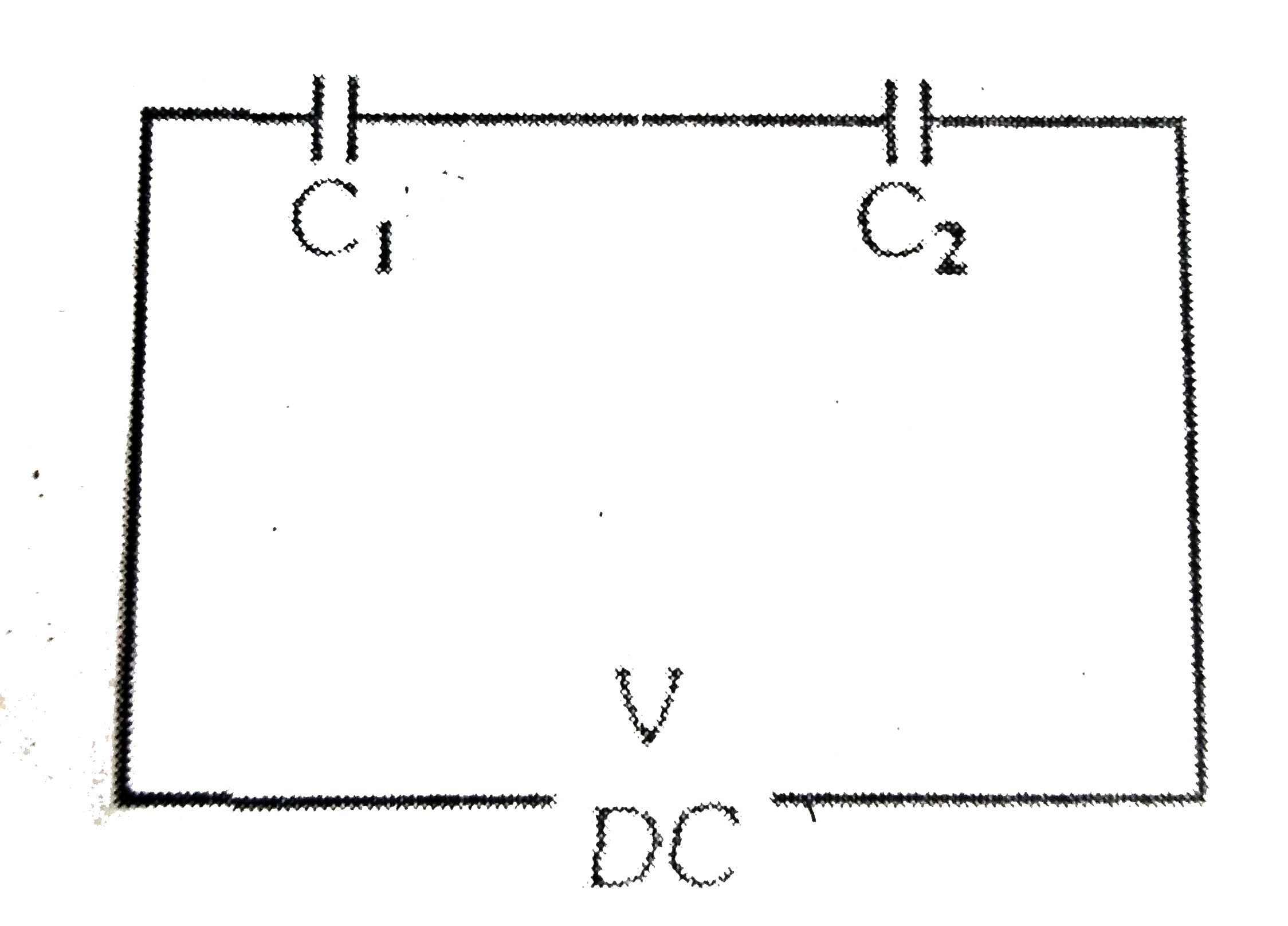
View SolutionA Capacitor of capacitance C1=1μF can withstand a maximum voltage V1=6.0 KV while another capacitor of capacitance C2=2.0μF withstands the maximum voltage V2=4.0 KV . What maximum will the system of these two capacitance withstand when connected in series as shown below .
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionTwo capacitor having capacitances 8μF and 16μF have breaking voltage 20V and 80V. They are combined in series. The maximum charge they can store individually in the combination is
View SolutionThree capacitors of 2μF,3μF and 6μF are joined in series and the combination is charged by means of a 24 volt battery. The potential difference between the plates of the 6μF capacitor is
View Solution
