A particle is dropped from point A at a certain height from ground. It falls freely and passes through thre points B,C and D with BC=CD. The time taken by the particle to move from B to CD is 2s and from C to D is 1s. The time taken to move from A to B is s
0.5s
1.5s
0.75s
0.25s
The correct Answer is:A
To solve the problem step by step, we will use the equations of motion for a freely falling body.
Step 1: Understand the motion from A to B
The particle is dropped from point A, so the initial velocity (u) at point A is 0. The distance from A to B is denoted as h1.
Using the second equation of motion:
s=ut+12gt2
For the motion from A to B:
h1=0⋅t+12gt2(where t is the time taken from A to B)
This simplifies to:
h1=12gt2(1)
Step 2: Analyze the motion from B to C
The time taken to move from B to C is given as 2 seconds. The distance BC is denoted as h2.
Using the second equation of motion again:
h2=vB⋅t+12gt2
Where vB is the velocity at point B. We can find vB using the third equation of motion:
v2B=u2+2as⇒v2B=0+2gh1⇒vB=√2gh1(2)
Now substituting vB into the equation for h2:
h2=√2gh1⋅2+12g(22)
This simplifies to:
h2=2√2gh1+2g(3)
Step 3: Analyze the motion from C to D
The time taken to move from C to D is given as 1 second. The distance CD is also h2.
Using the second equation of motion:
h2=vC⋅t+12gt2
Where vC is the velocity at point C. We can find vC using:
vC=vB+gtB⇒vC=√2gh1+g⋅2⇒vC=√2gh1+2g(4)
Now substituting vC into the equation for h2:
h2=(√2gh1+2g)⋅1+12g(12)
This simplifies to:
h2=√2gh1+2g+12g⇒h2=√2gh1+52g(5)
Step 4: Equate equations (3) and (5)
From equations (3) and (5), we can set them equal:
2√2gh1+2g=√2gh1+52g
Rearranging gives:
2√2gh1−√2gh1=52g−2g
This simplifies to:
√2gh1=12g
Squaring both sides:
2gh1=14g2⇒h1=g8(6)
Step 5: Find the time taken from A to B
Substituting h1 back into equation (1):
h1=12gt2⇒g8=12gt2
Dividing both sides by g (assuming g≠0):
18=12t2
Multiplying both sides by 2:
14=t2
Taking the square root:
t=12 seconds
Final Answer
The time taken to move from A to B is 0.5 seconds.
---
The particle is dropped from point A, so the initial velocity (u) at point A is 0. The distance from A to B is denoted as h1.
s=ut+12gt2
For the motion from A to B:
h1=0⋅t+12gt2(where t is the time taken from A to B)
This simplifies to:
h1=12gt2(1)
The time taken to move from B to C is given as 2 seconds. The distance BC is denoted as h2.
h2=vB⋅t+12gt2
Where vB is the velocity at point B. We can find vB using the third equation of motion:
v2B=u2+2as⇒v2B=0+2gh1⇒vB=√2gh1(2)
Now substituting vB into the equation for h2:
h2=√2gh1⋅2+12g(22)
This simplifies to:
h2=2√2gh1+2g(3)
The time taken to move from C to D is given as 1 second. The distance CD is also h2.
h2=vC⋅t+12gt2
Where vC is the velocity at point C. We can find vC using:
vC=vB+gtB⇒vC=√2gh1+g⋅2⇒vC=√2gh1+2g(4)
Now substituting vC into the equation for h2:
h2=(√2gh1+2g)⋅1+12g(12)
This simplifies to:
h2=√2gh1+2g+12g⇒h2=√2gh1+52g(5)
From equations (3) and (5), we can set them equal:
2√2gh1+2g=√2gh1+52g
Rearranging gives:
2√2gh1−√2gh1=52g−2g
This simplifies to:
√2gh1=12g
Squaring both sides:
2gh1=14g2⇒h1=g8(6)
Substituting h1 back into equation (1):
h1=12gt2⇒g8=12gt2
Dividing both sides by g (assuming g≠0):
18=12t2
Multiplying both sides by 2:
14=t2
Taking the square root:
t=12 seconds
The time taken to move from A to B is 0.5 seconds.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A body is falling freely from a point A at certain height from the ground and passes through point B, C and D (vertically as shown) so that BC=CD. The time taken by the particle to move from B to C is 2 seconds and from C to D 1 second. Time taken to move from A to B in second is
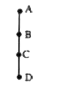
View SolutionA particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
View SolutionA particle is dropped from rest from a large height Assume g to be constant throughout the motion. The time taken by it to fall through successive distance of 1m each will be :
View SolutionLet A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View SolutionFor ground to ground projectile, time take by a particle to ge point O to point C is T1 and during the same motion time taken by the particle to ge from A to B is T2 then height 'h' is :

View SolutionA stone is dropped from a certain heitht which can reach the ground in 5s. It is stopped aftre 3s of its fall and then it is again released. The total time taken by the stone to reach the ground will be .
View SolutionA paricle performs S.H.M. with time period T. The time taken by the particle to move from hall the amplitude to the maximum dispalcement is T2
View SolutionA particle executing a simple harmonic motion has a period of 6 s. The time taken by the particle to move from the mean position to half the amplitude, starting from the mean position is
View SolutionA particle executes SHM with a time period of 4s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionA particle is released from a height S. At certain height its kinetic energy is three times its potential energy. The height and speed of the particle at that instant are respectively
View Solution
