A particle is moving in x−y plane with y=x2 and Vx=4−2t. The displacement versus time graph of the particle would be
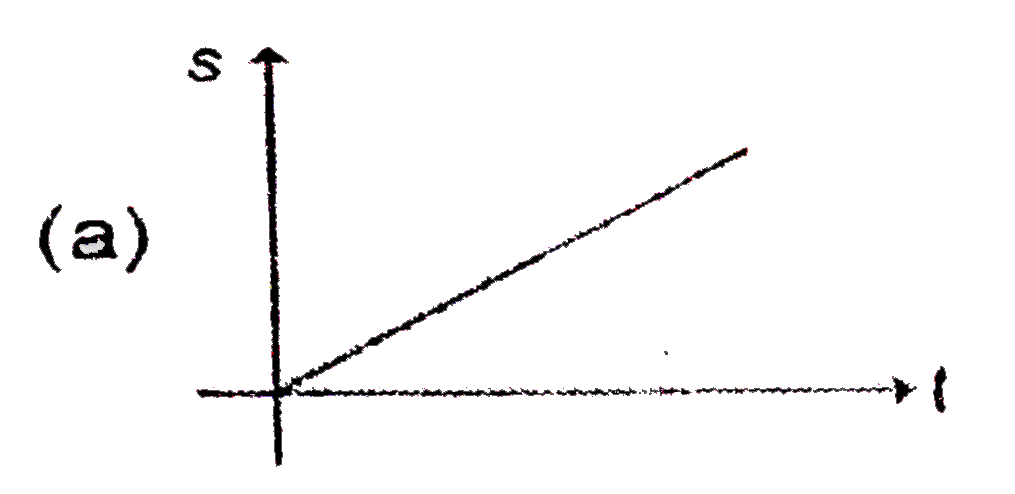

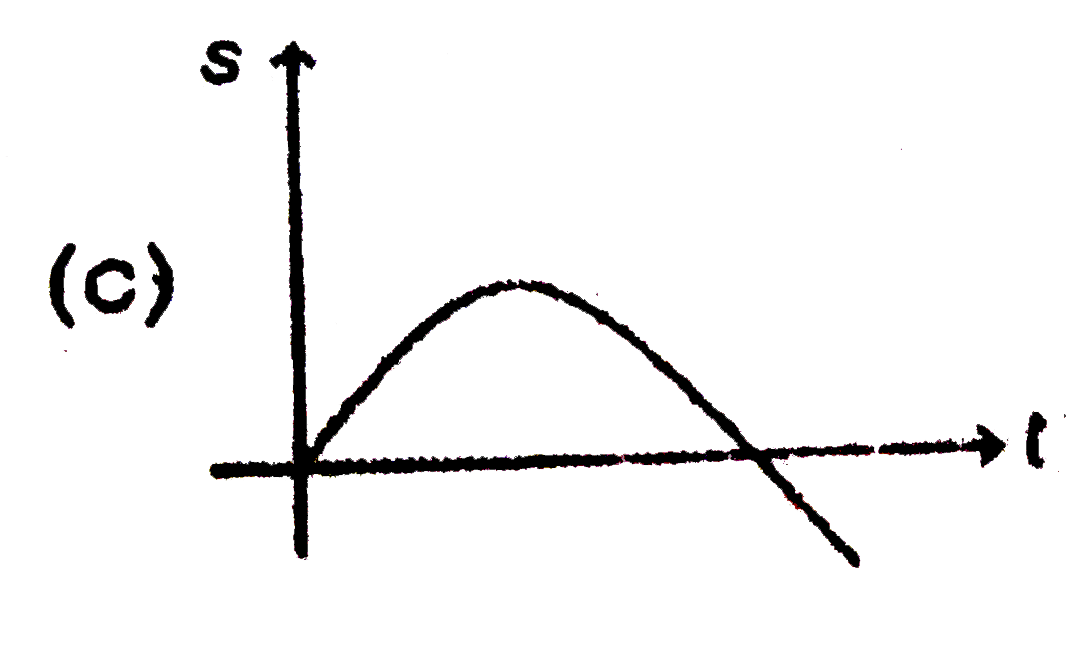
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of the particle in the x-y plane and derive the displacement versus time graph.
Step 1: Understand the given equations
The particle is moving in the x-y plane with the equation for y given as:
y=x2
And the velocity in the x-direction is given as:
Vx=4−2t
Step 2: Relate velocity to displacement
The velocity Vx can be expressed as the derivative of displacement x with respect to time t:
Vx=dxdt
Thus, we can write:
dxdt=4−2t
Step 3: Rearrange the equation for integration
Rearranging the equation gives us:
dx=(4−2t)dt
Step 4: Integrate both sides
Now, we will integrate both sides. The left side integrates to x, and the right side can be integrated term by term:
∫dx=∫(4−2t)dt
This results in:
x=4t−t2+C
where C is the constant of integration.
Step 5: Determine the constant of integration
Assuming the particle starts at the origin when t=0, we have:
x(0)=0⟹0=4(0)−(0)2+C⟹C=0
Thus, the equation simplifies to:
x=4t−t2
Step 6: Analyze the equation of motion
The equation x=4t−t2 is a quadratic equation in terms of t. This represents a parabola opening downwards.
Step 7: Determine the displacement versus time graph
Since x is a quadratic function of t, the displacement versus time graph will be a parabola. The vertex of this parabola can be found using the formula t=−b2a where a=−1 and b=4:
t=−42(−1)=2
At t=2:
x=4(2)−(2)2=8−4=4
Thus, the vertex of the parabola is at the point (2, 4).
Conclusion
The displacement versus time graph of the particle is a downward-opening parabola with its vertex at (2, 4).
The particle is moving in the x-y plane with the equation for y given as:
y=x2
And the velocity in the x-direction is given as:
Vx=4−2t
The velocity Vx can be expressed as the derivative of displacement x with respect to time t:
Vx=dxdt
Thus, we can write:
dxdt=4−2t
Rearranging the equation gives us:
dx=(4−2t)dt
Now, we will integrate both sides. The left side integrates to x, and the right side can be integrated term by term:
∫dx=∫(4−2t)dt
This results in:
x=4t−t2+C
where C is the constant of integration.
Assuming the particle starts at the origin when t=0, we have:
x(0)=0⟹0=4(0)−(0)2+C⟹C=0
Thus, the equation simplifies to:
x=4t−t2
The equation x=4t−t2 is a quadratic equation in terms of t. This represents a parabola opening downwards.
Since x is a quadratic function of t, the displacement versus time graph will be a parabola. The vertex of this parabola can be found using the formula t=−b2a where a=−1 and b=4:
t=−42(−1)=2
At t=2:
x=4(2)−(2)2=8−4=4
Thus, the vertex of the parabola is at the point (2, 4).
The displacement versus time graph of the particle is a downward-opening parabola with its vertex at (2, 4).
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle id moving in xy - plane with y=x/2andvx=4−2t. Choose the correct options.
View SolutionFigure shows the displacement time graph of a particle moving on the X-axis

View SolutionFigure shows the displacement-time graph of a particle moving on the X-axis

View SolutionA particle moves in x−y plane according to the law x=4sin6tandy=4(1−cos6t). The distance traversed by the particle in 4 second is (x&y are in meters)
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
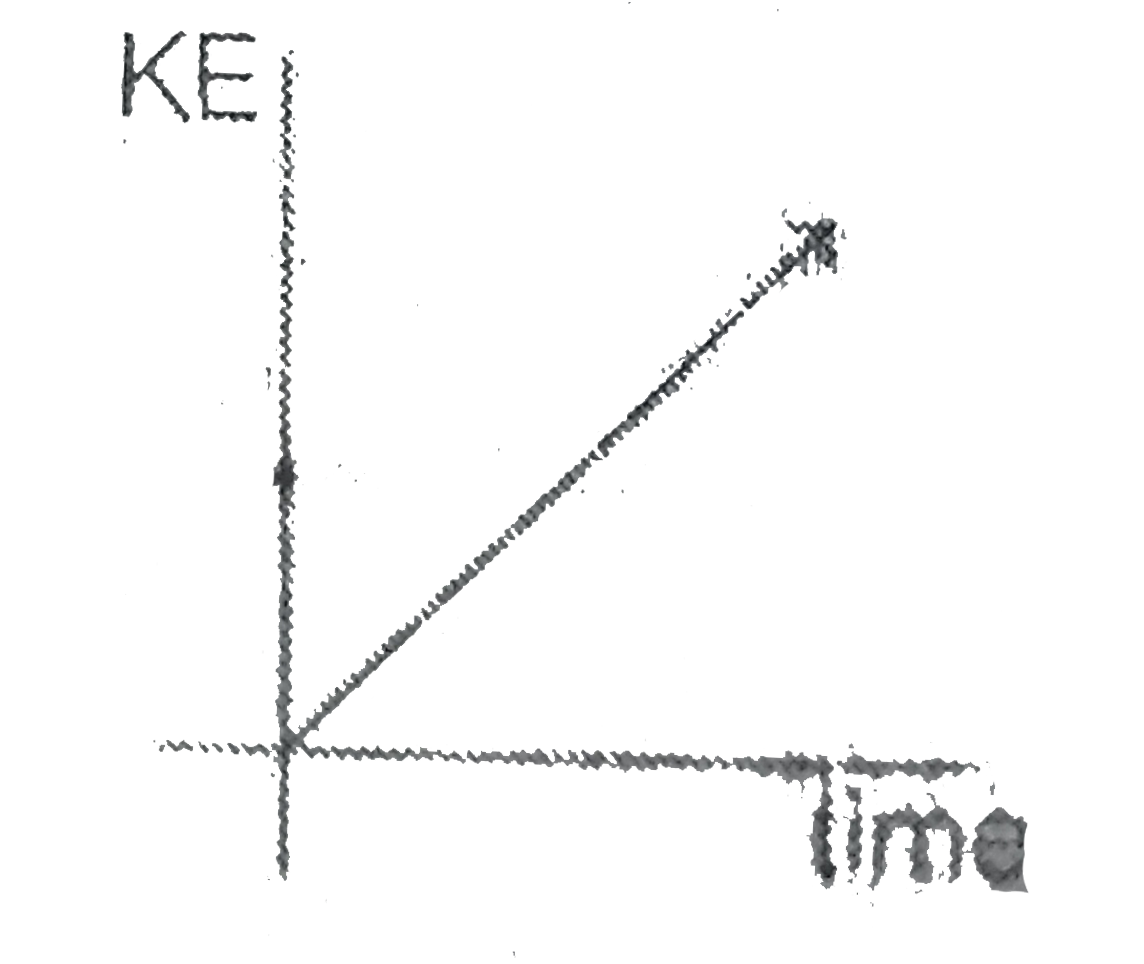
View SolutionThe acceleration versus time graph of a particle moving in a straight line is show in. The velocity-time graph of the particle would be
 .
.
View SolutionThe co-ordinates of a particle moving in xy-plane vary with time as x=at2,y=bt. The locus of the particle is :
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View SolutionThe coordinates of a particle moving in XY-plane vary with time as x=4t2,y=2t. The locus of the particle is a : -
View SolutionThe coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
View Solution
