A gas is expanded to double its volume by two different processes. One is isobaric and the other is isothermal. Let W1 and W2 be the respective work done, then find W1 and W2
A) W2=W1ln(2)
B) W2=W1ln(2)
C) W2=W12
D) Data is insufficient
The correct Answer is:A
To solve the problem of finding the work done in two different processes (isobaric and isothermal) when a gas is expanded to double its volume, we can follow these steps:
Step 1: Understand the Processes
1. Isobaric Process: In an isobaric process, the pressure remains constant. The work done W1 during an isobaric expansion can be calculated using the formula:
W1=PΔV
where ΔV is the change in volume.
2. Isothermal Process: In an isothermal process, the temperature remains constant. The work done W2 during an isothermal expansion can be calculated using the formula:
W2=nRTln(VfVi)
where n is the number of moles, R is the gas constant, Vf is the final volume, and Vi is the initial volume.
Step 2: Calculate Work Done in Isobaric Process
1. Let the initial volume Vi=V1 and the final volume Vf=V2=2V1.
2. The change in volume ΔV=Vf−Vi=2V1−V1=V1.
3. Thus, the work done in the isobaric process is:
W1=P⋅V1
Step 3: Calculate Work Done in Isothermal Process
1. For the isothermal process, using the same initial and final volumes:
W2=nRTln(VfVi)=nRTln(2V1V1)=nRTln(2)
Summary of Results
- The work done in the isobaric process is:
W1=P⋅V1
- The work done in the isothermal process is:
W2=nRTln(2)
Step 4: Relationship Between W1 and W2
From the derived equations, we can see that:
W_2 = W_1 \cdot \ln(2) \quad \text{(if we express P intermsof nRT/V_1 )}
Final Answer
- W1=P⋅V1
- W2=nRTln(2)
1. Isobaric Process: In an isobaric process, the pressure remains constant. The work done W1 during an isobaric expansion can be calculated using the formula:
W1=PΔV
where ΔV is the change in volume.
W2=nRTln(VfVi)
where n is the number of moles, R is the gas constant, Vf is the final volume, and Vi is the initial volume.
1. Let the initial volume Vi=V1 and the final volume Vf=V2=2V1.
2. The change in volume ΔV=Vf−Vi=2V1−V1=V1.
3. Thus, the work done in the isobaric process is:
W1=P⋅V1
1. For the isothermal process, using the same initial and final volumes:
W2=nRTln(VfVi)=nRTln(2V1V1)=nRTln(2)
- The work done in the isobaric process is:
W1=P⋅V1
- The work done in the isothermal process is:
W2=nRTln(2)
From the derived equations, we can see that:
W_2 = W_1 \cdot \ln(2) \quad \text{(if we express P intermsof nRT/V_1 )}
- W1=P⋅V1
- W2=nRTln(2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
A gas expands from i to f along the three paths indicated. The work done along the three paths denoted by W1,W2andW3 have the relationship
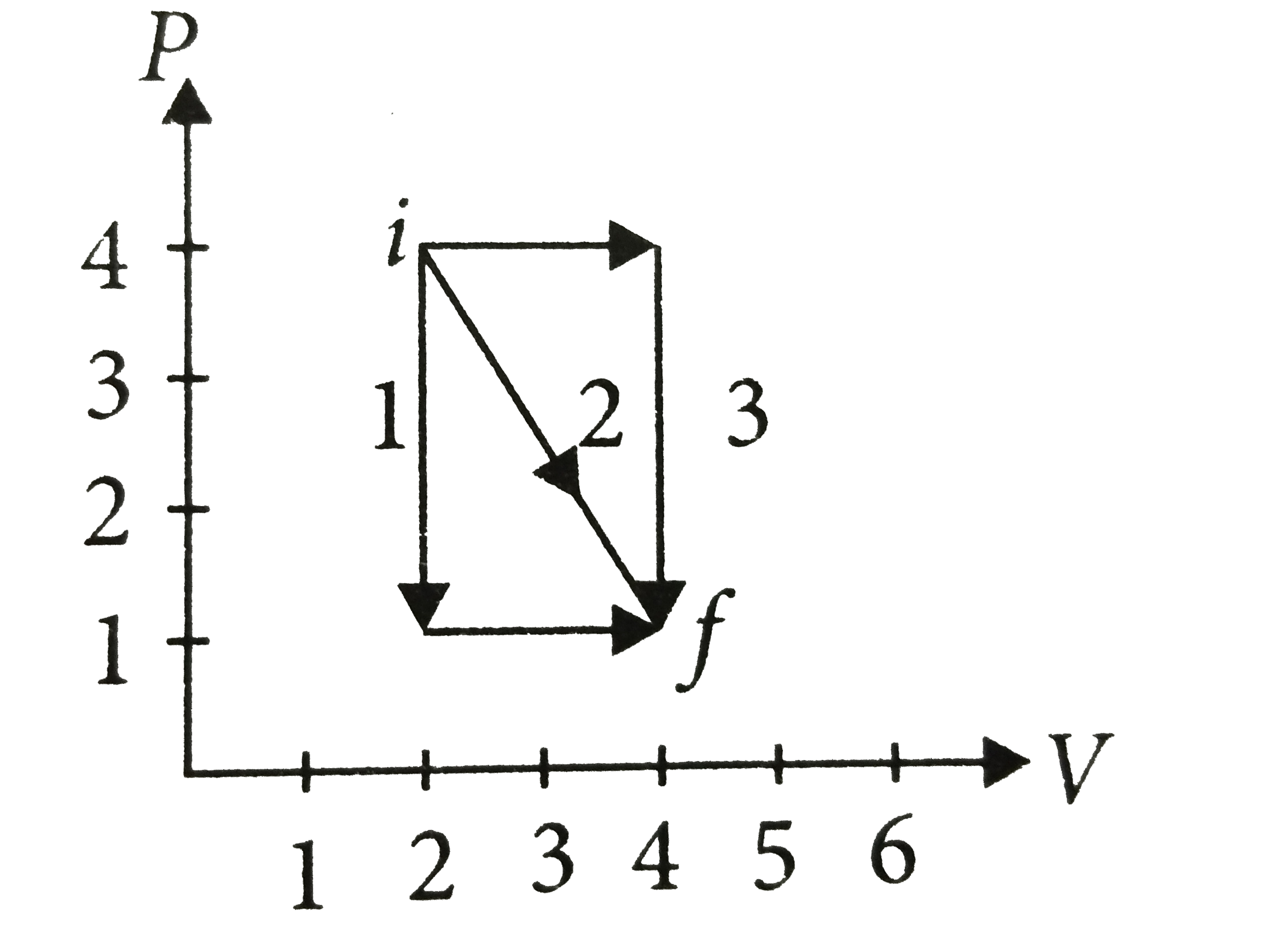 AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
W1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.

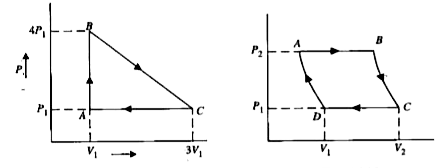
View SolutionAn ideal gas undergoes a thermodynamic process as shown in Fig. The process consists of two isobaric and two isothermal steps. Show that the network done during the whole process is
W(Net)=P1(V2−V1)logeP2P1
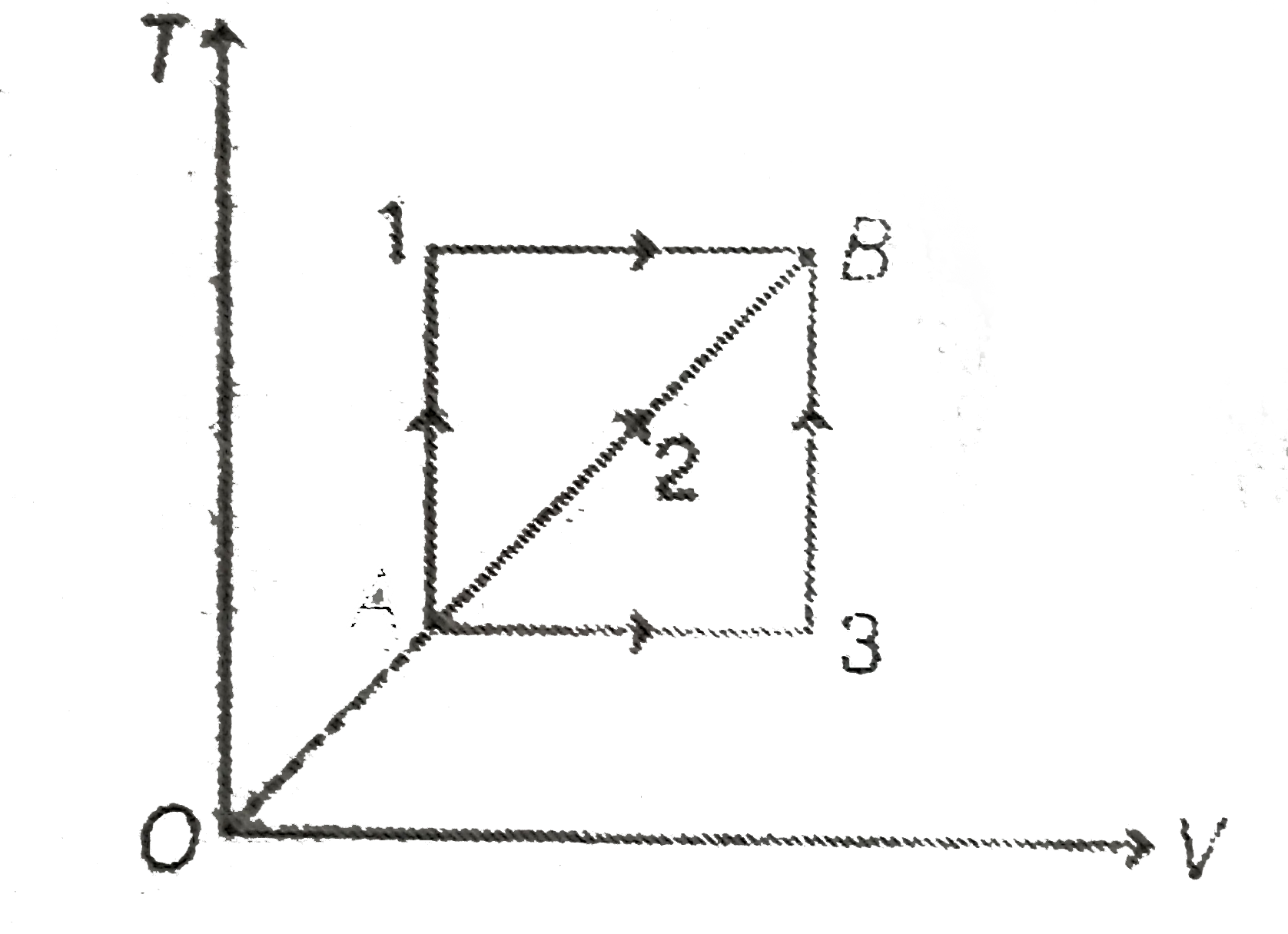
View SolutionA givne mass of a gas expands from a state A to the state B by three paths 1, 2 and 3 as shown in T-V indicator diagram. If W1,W2 and W3 respectively be the work done by the gas along the three paths, then
View SolutionA given mass of gas expands from state A to state b by three paths 1,2, and 3 as shown in the figure below. If w1,w2 and w3, respectively, be the work done by the gas along three paths, then
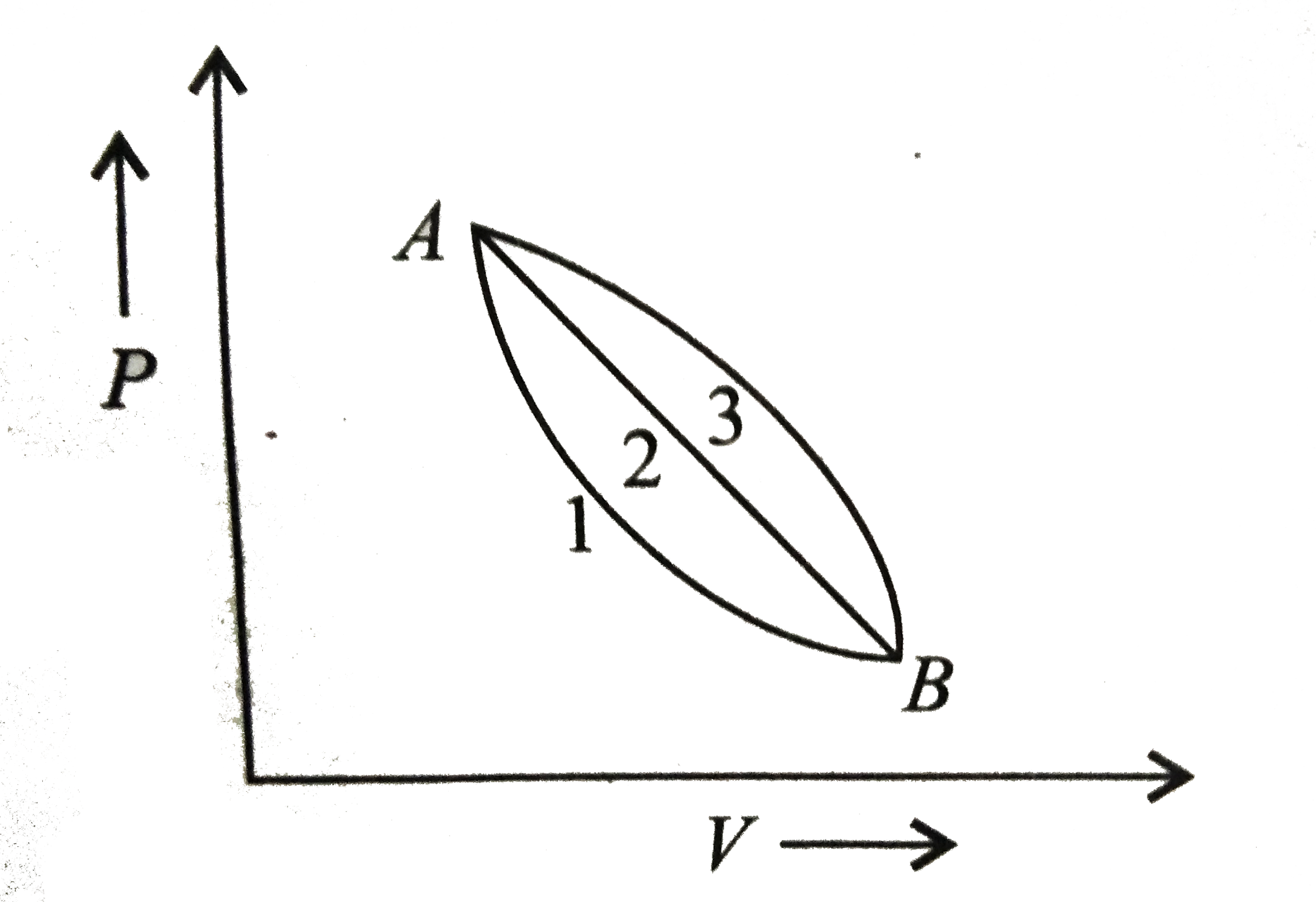
View SolutionA given mass of gas expands from state A to state B by three paths 1,2, and 3 as shown in the figure below. If w1,w2 and w3, respectively, be the work done by the gas along three paths, then

View SolutionLet Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
View SolutionWork done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
View Solution
