The weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
w1<w2<w3
w1=w2=w3
w1<w2<w3
w1>w2>w3
The correct Answer is:A
To solve the problem regarding the weight of an object in a coal mine, at sea level, and at the top of a mountain, we need to understand how gravitational force (weight) varies with altitude and depth.
1. Understanding Weight:
The weight of an object is given by the formula:
W=mg
where W is the weight, m is the mass of the object, and g is the acceleration due to gravity.
2. Weight at Sea Level (W2):
At sea level, the value of g is approximately 9.81m/s2. Therefore, the weight of the object at sea level is:
W2=mg
3. Weight in a Coal Mine (W1):
When we go deep into a coal mine, we are moving below the Earth's surface. The value of g decreases slightly as we go deeper due to the reduction in the effective mass of the Earth above us. Thus, the weight in the coal mine is:
W_1 = m g_1 \quad \text{(where g_1 < g )}
This means W1<W2.
4. Weight at the Top of a Mountain (W3):
At the top of a mountain, we are at a higher altitude, which also causes the value of g to decrease. Therefore, the weight at the top of the mountain is:
W_3 = m g_3 \quad \text{(where g_3 < g )}
This means W3<W2.
5. Comparing the Weights:
From the above analysis, we can conclude:
- W1<W2 (Weight in coal mine is less than at sea level)
- W3<W2 (Weight at the top of the mountain is less than at sea level)
6. Final Conclusion:
Since both W1 and W3 are less than W2, we can summarize the relationship as:
W1<W2>W3
The weight of an object is given by the formula:
W=mg
where W is the weight, m is the mass of the object, and g is the acceleration due to gravity.
At sea level, the value of g is approximately 9.81m/s2. Therefore, the weight of the object at sea level is:
W2=mg
When we go deep into a coal mine, we are moving below the Earth's surface. The value of g decreases slightly as we go deeper due to the reduction in the effective mass of the Earth above us. Thus, the weight in the coal mine is:
W_1 = m g_1 \quad \text{(where g_1 < g )}
This means W1<W2.
At the top of a mountain, we are at a higher altitude, which also causes the value of g to decrease. Therefore, the weight at the top of the mountain is:
W_3 = m g_3 \quad \text{(where g_3 < g )}
This means W3<W2.
From the above analysis, we can conclude:
- W1<W2 (Weight in coal mine is less than at sea level)
- W3<W2 (Weight at the top of the mountain is less than at sea level)
Since both W1 and W3 are less than W2, we can summarize the relationship as:
W1<W2>W3
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
The work done in moving a particle in the gravitational field of earth from point A to point B along three different paths 1,2 and 3 are W1,W2 and W3 respectively , then
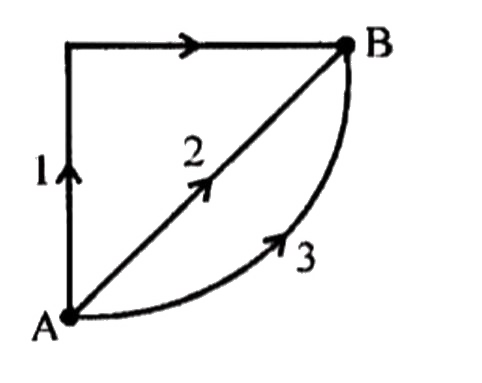
View SolutionW1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.

View Solution
Knowledge Check
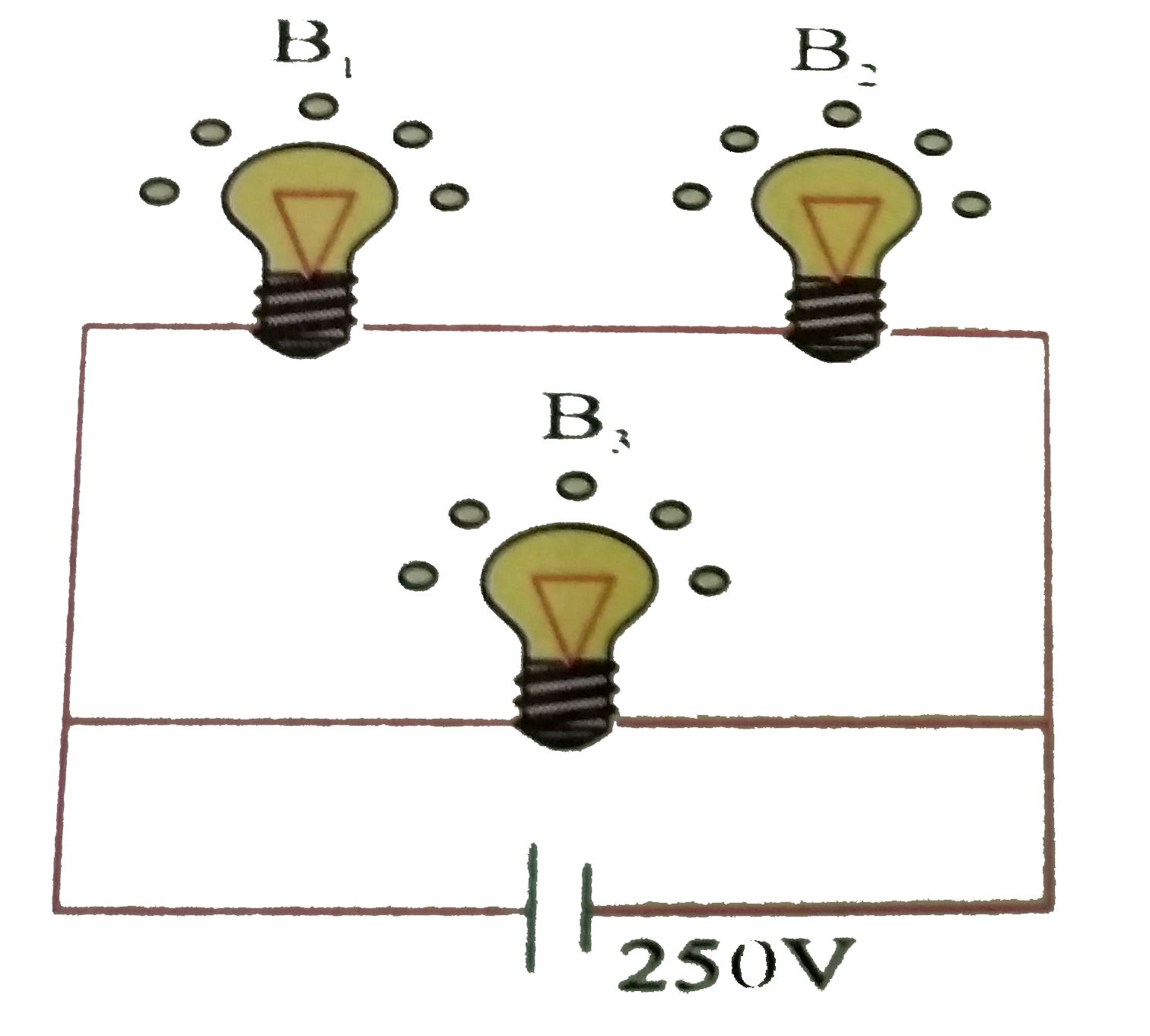
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3
Why it is cooler at the top of a mountain than at sea level?
View SolutionA given mass of a gas expands from the state A to the state B by three paths 1,2 and 3 as shown in the figure, If W1,W2 and W3 respectively be the work done by the gas along the three paths then

View SolutionA given mass of gas expands from state A to state B by three paths 1, 2, and 3 as shown in the figure :
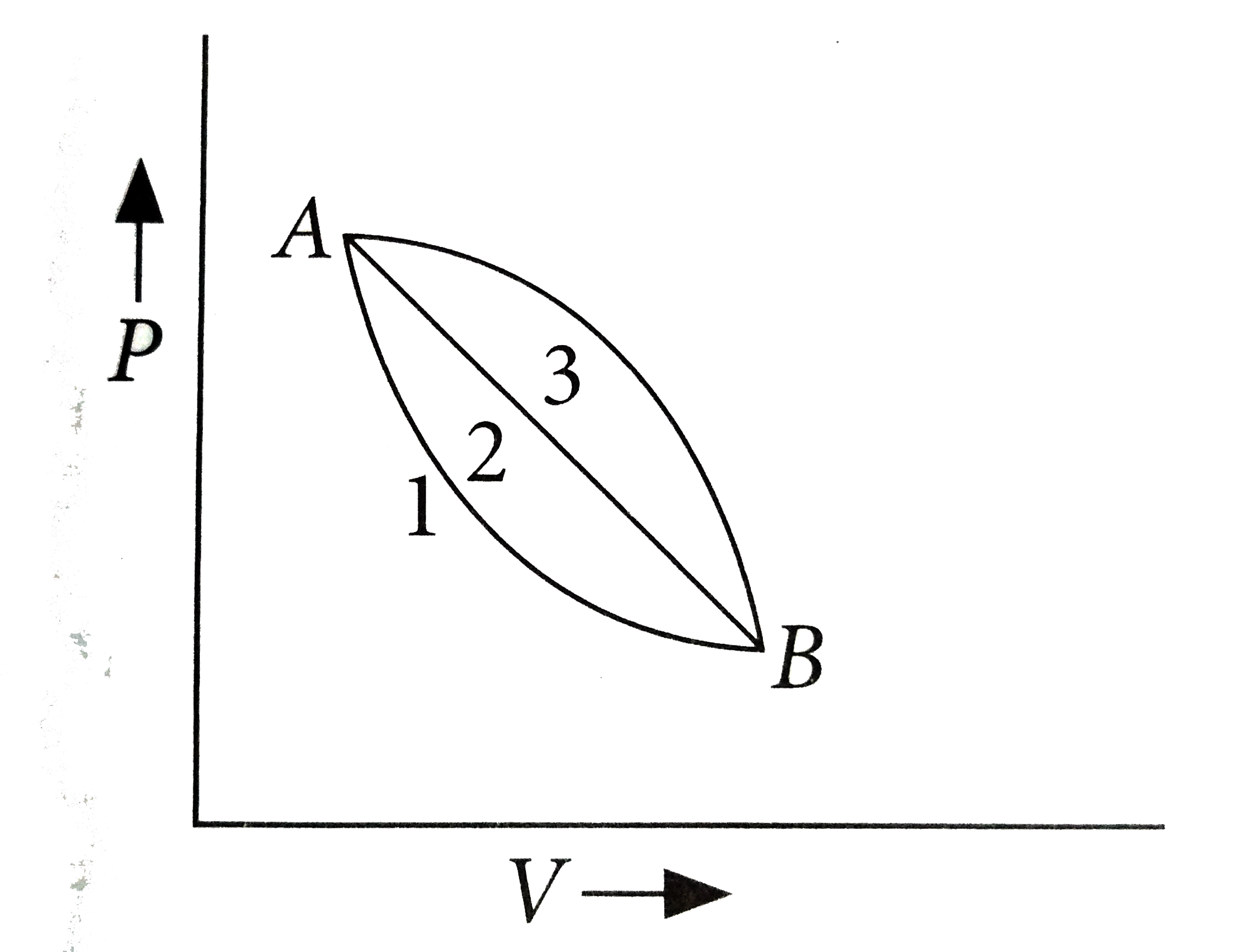
If w1,w2andw3 respectively, be the work done by the gas along three paths, then
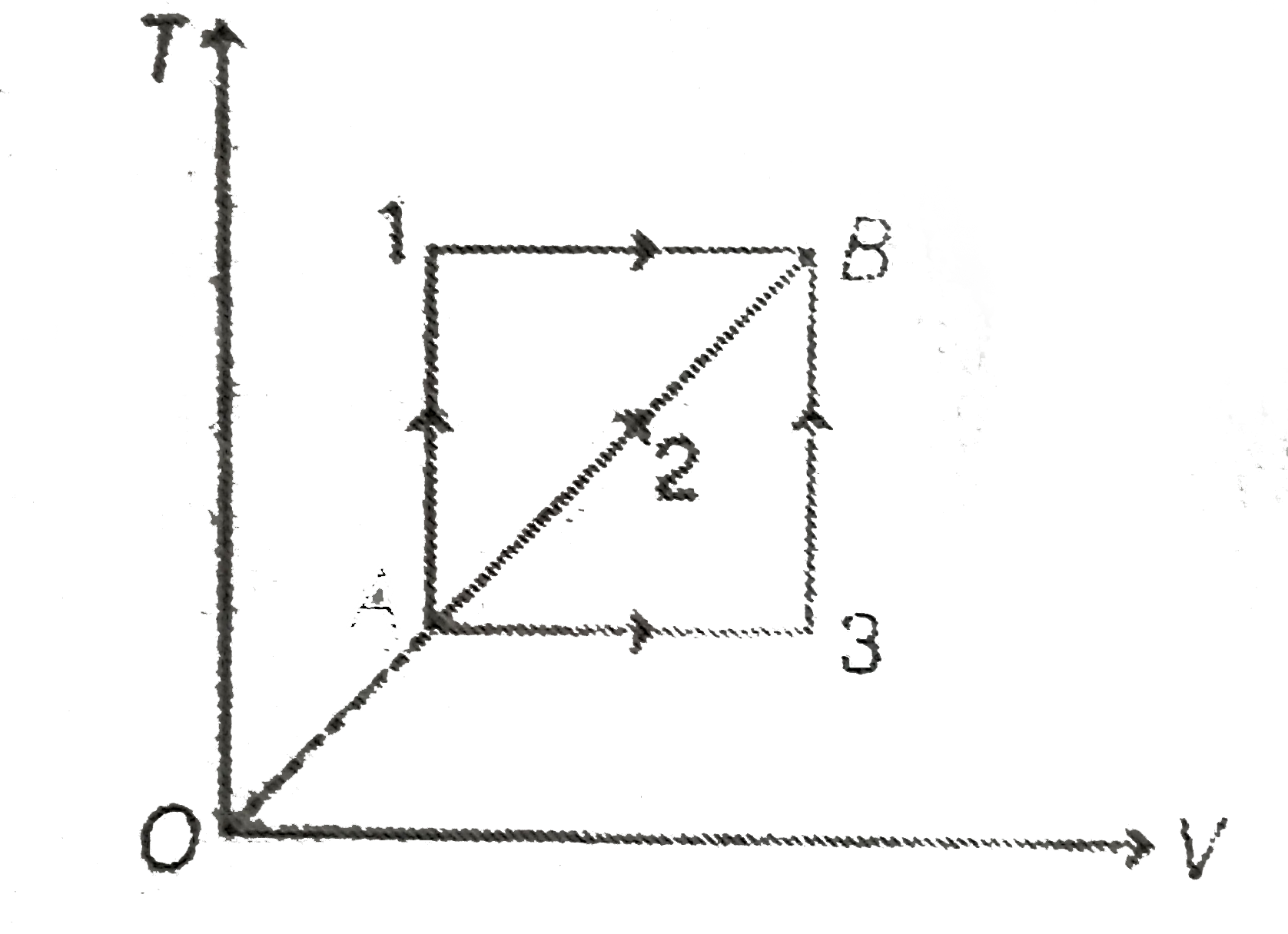
View SolutionA givne mass of a gas expands from a state A to the state B by three paths 1, 2 and 3 as shown in T-V indicator diagram. If W1,W2 and W3 respectively be the work done by the gas along the three paths, then
View SolutionA given mass of gas expands from state A to state b by three paths 1,2, and 3 as shown in the figure below. If w1,w2 and w3, respectively, be the work done by the gas along three paths, then
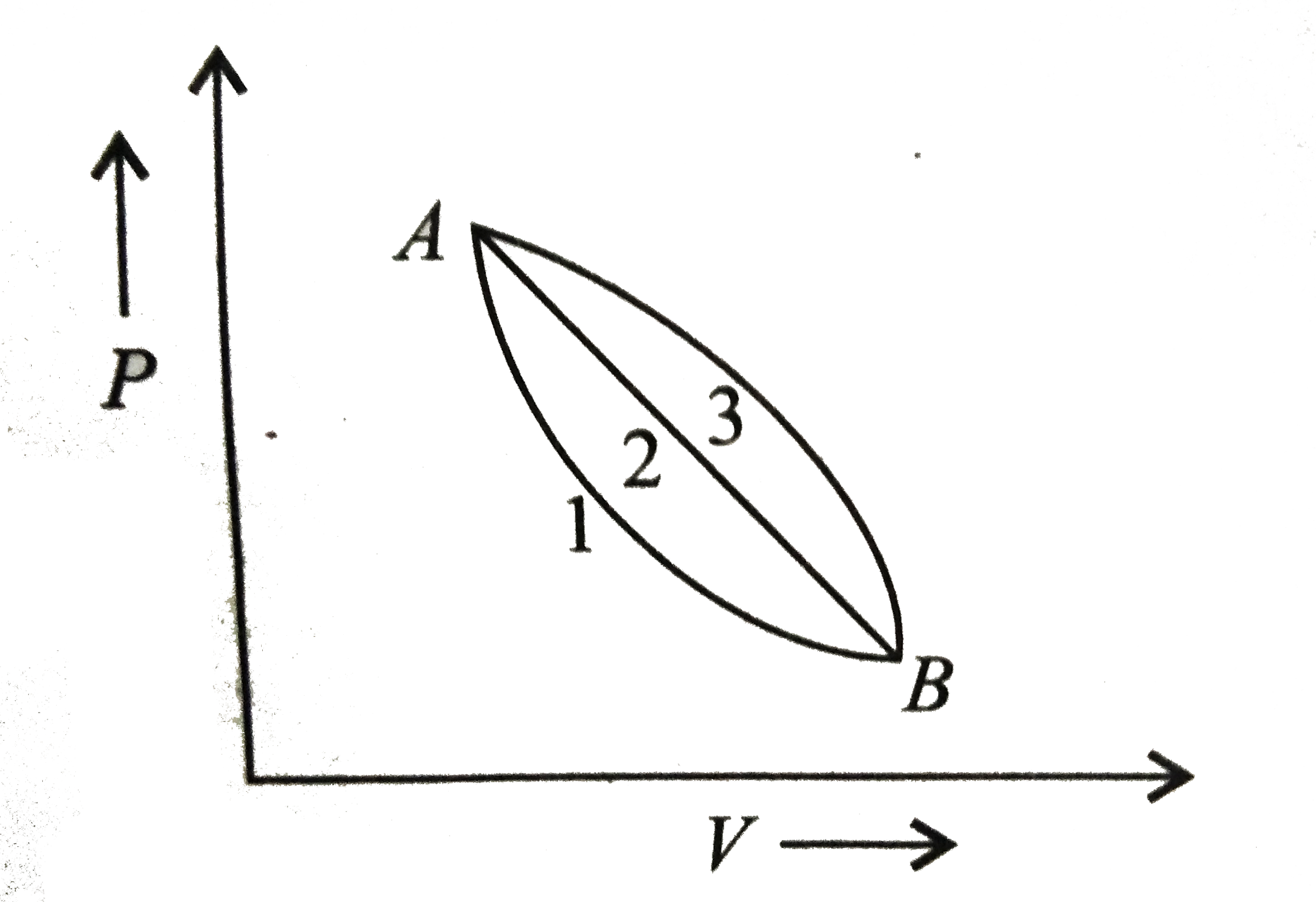
View SolutionGiven T-p curve for three processes. Work done in process 1, 2 and 3 (if initial and final pressure are same for all processes) is W1,W2 and W3 respectively. Correct order is

View Solution
