P-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
4R
2.5R
3R
4R3
The correct Answer is:C
To solve the problem regarding the molar heat capacity of a diatomic gas in a process represented by a straight line on a P-V diagram, we can follow these steps:
Step 1: Understand the P-V Diagram
The problem states that the P-V diagram of the diatomic gas is a straight line passing through the origin. This indicates a linear relationship between pressure (P) and volume (V).
Hint: A straight line through the origin implies that P is directly proportional to V.
Step 2: Apply the First Law of Thermodynamics
According to the first law of thermodynamics, we have:
Q=U+W
Where:
- Q is the heat added to the system,
- U is the internal energy,
- W is the work done by the system.
Hint: Remember that the internal energy change U for an ideal gas can be expressed in terms of molar heat capacity.
Step 3: Express the Work Done
For a process represented by a straight line on a P-V diagram, the work done W can be calculated as the area under the curve. Since it forms a triangle, the area can be calculated as:
W=12×base×height=12×V×P
Hint: The area of a triangle is half the product of its base and height.
Step 4: Relate Pressure, Volume, and Temperature
Using the ideal gas law:
PV=nRΔT
This can be substituted into the work done expression.
Hint: Use the ideal gas law to express PV in terms of temperature.
Step 5: Substitute into the First Law Equation
Substituting the expressions for Q, U, and W into the first law equation gives:
nCΔT=nCvΔT+nRΔT2
Hint: Factor out common terms to simplify the equation.
Step 6: Simplify the Equation
Taking nΔT common from both sides, we get:
C=Cv+R2
Hint: Isolate C to find the relationship between heat capacities.
Step 7: Substitute the Value of Cv
For a diatomic gas, the molar heat capacity at constant volume Cv is:
Cv=52R
Substituting this into the equation gives:
C=52R+R2=3R
Hint: Ensure you perform the arithmetic correctly when combining terms.
Step 8: Conclusion
Thus, the molar heat capacity C for the diatomic gas in this process is:
C=3R
Final Answer: The correct option is 3R.
---
The problem states that the P-V diagram of the diatomic gas is a straight line passing through the origin. This indicates a linear relationship between pressure (P) and volume (V).
According to the first law of thermodynamics, we have:
Q=U+W
Where:
- Q is the heat added to the system,
- U is the internal energy,
- W is the work done by the system.
For a process represented by a straight line on a P-V diagram, the work done W can be calculated as the area under the curve. Since it forms a triangle, the area can be calculated as:
W=12×base×height=12×V×P
Using the ideal gas law:
PV=nRΔT
This can be substituted into the work done expression.
Substituting the expressions for Q, U, and W into the first law equation gives:
nCΔT=nCvΔT+nRΔT2
Taking nΔT common from both sides, we get:
C=Cv+R2
For a diatomic gas, the molar heat capacity at constant volume Cv is:
Cv=52R
Substituting this into the equation gives:
C=52R+R2=3R
Thus, the molar heat capacity C for the diatomic gas in this process is:
C=3R
Topper's Solved these Questions
Similar Questions
If the P-V diagram of a diatomic gas is plotted, it is a straight line passing through the origin. The molar heat capacity of the gas in the process is IR, where I is an integer. Find the value of I.
View SolutionThe molar heat capacity for an ideal gas
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionThe variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the figure . The molar species heat of the gas during this process is
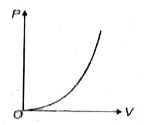
View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionIn a thermodynamic process on an ideal diatomic gas, work done by the gas is η times the heat supplied (η<1). The molar heat capacity of the gas for the process is
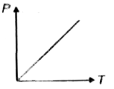
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure . The molar heat capacity of gas during this process is [R is gas constant]
View SolutionTemperature of two moles of a monoatomic gas is increased by 300K in the process p∝V. Find
(a) molar heat capacity of the gas in the given process
(b) heat required in the given process.
View Solution