In a thermodynamic process on an ideal diatomic gas, work done by the gas is η times the heat supplied (η<1). The molar heat capacity of the gas for the process is
5R2
5ηR2
5R2(1−η)
5R(1−η)2
The correct Answer is:C
To find the molar heat capacity of an ideal diatomic gas in a thermodynamic process where the work done by the gas is η times the heat supplied (with η<1), we can follow these steps:
1. Understand the First Law of Thermodynamics:
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat supplied, dU is the change in internal energy, and dW is the work done by the gas.
2. Express Work Done:
According to the problem, the work done by the gas is given by:
dW=η⋅dQ
3. Substitute Work Done into the First Law:
Substitute dW into the first law:
dQ=dU+η⋅dQ
4. Rearrange to Find Change in Internal Energy:
Rearranging gives:
dU=dQ−η⋅dQ=(1−η)dQ
5. Relate Change in Internal Energy to Temperature Change:
For an ideal gas, the change in internal energy can be expressed as:
dU=nCvdT
where Cv is the molar heat capacity at constant volume.
6. Equate the Two Expressions for Change in Internal Energy:
From the previous steps, we have:
nCvdT=(1−η)dQ
7. Express Heat Supplied:
The heat supplied can be expressed as:
dQ=nCdT
where C is the molar heat capacity for the process.
8. Substitute dQ in the Equation:
Substitute dQ into the equation:
nCvdT=(1−η)(nCdT)
9. Cancel ndT from Both Sides:
Assuming n≠0 and dT≠0, we can cancel ndT:
Cv=(1−η)C
10. Solve for Molar Heat Capacity C:
Rearranging gives:
C=Cv1−η
11. Substitute Cv for a Diatomic Gas:
For a diatomic ideal gas, the molar heat capacity at constant volume is:
Cv=52R
Therefore,
C=52R1−η
Final Result:
The molar heat capacity C for the process is:
C=5R2(1−η)
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat supplied, dU is the change in internal energy, and dW is the work done by the gas.
According to the problem, the work done by the gas is given by:
dW=η⋅dQ
Substitute dW into the first law:
dQ=dU+η⋅dQ
Rearranging gives:
dU=dQ−η⋅dQ=(1−η)dQ
For an ideal gas, the change in internal energy can be expressed as:
dU=nCvdT
where Cv is the molar heat capacity at constant volume.
From the previous steps, we have:
nCvdT=(1−η)dQ
The heat supplied can be expressed as:
dQ=nCdT
where C is the molar heat capacity for the process.
Substitute dQ into the equation:
nCvdT=(1−η)(nCdT)
Assuming n≠0 and dT≠0, we can cancel ndT:
Cv=(1−η)C
Rearranging gives:
C=Cv1−η
For a diatomic ideal gas, the molar heat capacity at constant volume is:
Cv=52R
Therefore,
C=52R1−η
The molar heat capacity C for the process is:
C=5R2(1−η)
Topper's Solved these Questions
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:Assignment (Section-C) Objective Type Questions (More than one option are correct)
Explore 11 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:Assignment (Section-D) Linked comprehension Type questions
Explore 3 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:Assignment (Section-A) Objective Type Questions (one option is correct)
Explore 50 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTE ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-J) Akash Challengers Questions
Explore 7 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTE ENGLISHChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
The molar heat capacity for an ideal gas
View SolutionThe thermodynamic process in which no work is done on or by the gas is
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionAn ideal gas (γ=1.5) undergoes a thermodynamic process in which the temperature and pressure of the gas are related as T−1P2= constant. The molar heat capacity of the gas during the process is
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionFor a certain process, pressure of diatomic gas varies according to the relation P=aV2, where a is constant. What is the molar heat capacity of the gas for this process ?
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure . The molar heat capacity of gas during this process is [R is gas constant]
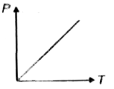
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View Solution
