The internal energy of a gas is given by U=2pV. It expands from V0 to 2V0 against a constant pressure p0. The heat absorbed by the gas in the process is
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between internal energy, work done, and heat absorbed.
According to the first law of thermodynamics, the relationship is given by:
ΔQ=ΔU+ΔW
where:
- ΔQ is the heat absorbed by the gas,
- ΔU is the change in internal energy,
- ΔW is the work done by the gas.
Step 2: Calculate the change in internal energy (ΔU).
The internal energy U is given by:
U=2pV
The gas expands from V0 to 2V0 against a constant pressure p0.
First, we find the initial and final internal energy:
- Initial internal energy when V=V0:
Ui=2p0V0
- Final internal energy when V=2V0:
Uf=2p0(2V0)=4p0V0
Now, we can calculate the change in internal energy:
ΔU=Uf−Ui=4p0V0−2p0V0=2p0V0
Step 3: Calculate the work done (ΔW).
Since the process is isobaric (constant pressure), the work done by the gas can be calculated as:
ΔW=pΔV
where ΔV=Vf−Vi=2V0−V0=V0.
Thus, the work done is:
ΔW=p0⋅V0
Step 4: Substitute ΔU and ΔW into the first law equation.
Now we can substitute our values into the first law of thermodynamics:
ΔQ=ΔU+ΔW=(2p0V0)+(p0V0)=3p0V0
Final Answer
The heat absorbed by the gas in the process is:
ΔQ=3p0V0
---
According to the first law of thermodynamics, the relationship is given by:
ΔQ=ΔU+ΔW
where:
- ΔQ is the heat absorbed by the gas,
- ΔU is the change in internal energy,
- ΔW is the work done by the gas.
The internal energy U is given by:
U=2pV
The gas expands from V0 to 2V0 against a constant pressure p0.
- Initial internal energy when V=V0:
Ui=2p0V0
- Final internal energy when V=2V0:
Uf=2p0(2V0)=4p0V0
ΔU=Uf−Ui=4p0V0−2p0V0=2p0V0
Since the process is isobaric (constant pressure), the work done by the gas can be calculated as:
ΔW=pΔV
where ΔV=Vf−Vi=2V0−V0=V0.
ΔW=p0⋅V0
Now we can substitute our values into the first law of thermodynamics:
ΔQ=ΔU+ΔW=(2p0V0)+(p0V0)=3p0V0
The heat absorbed by the gas in the process is:
ΔQ=3p0V0
Topper's Solved these Questions
Similar Questions
The internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
The heat absorbed by the gas in the process is
View SolutionThe internal energy of a gas is given by U=5+2PV. It expands from V0 to 2V0 against a constant pressure P0. The heat absorbed by the gas in the process is :-
View SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
What is the value of γ(=CP/CV) for the given gas?
View SolutionThe internal energy of a gas is given by U=1.5pV. It expands from 100cm3→200cm3 against a constant pressure of 1.0×105 Pa. calculate the heat absorbed by the gas in the process.
View SolutionThe internal energy of a gas is given by U=PV2. At constant volume, state of gas changes from (P0,V0) to (3P0,V0) then
View SolutionA diatomic gas with rigid molecules does 10J of work when expanded at constant pressure. The heat energy absorbed by the gas, in this process is ___________ (in J).
View SolutionA diatomic gas with rigid molecules does 10J of work when expanded at constant pressure. The heat energy absorbed by the gas, in this process is ___________ (in J).
View SolutionFigure shows the variation of internal energy (U) with the pressure (P) of 2.0 mole gas in cyclic process abcda.The temperature of gas at c and d are 300and500K respectively. The heat absorbed by the gas during the process is X×10Rln2 . Find the value of x.
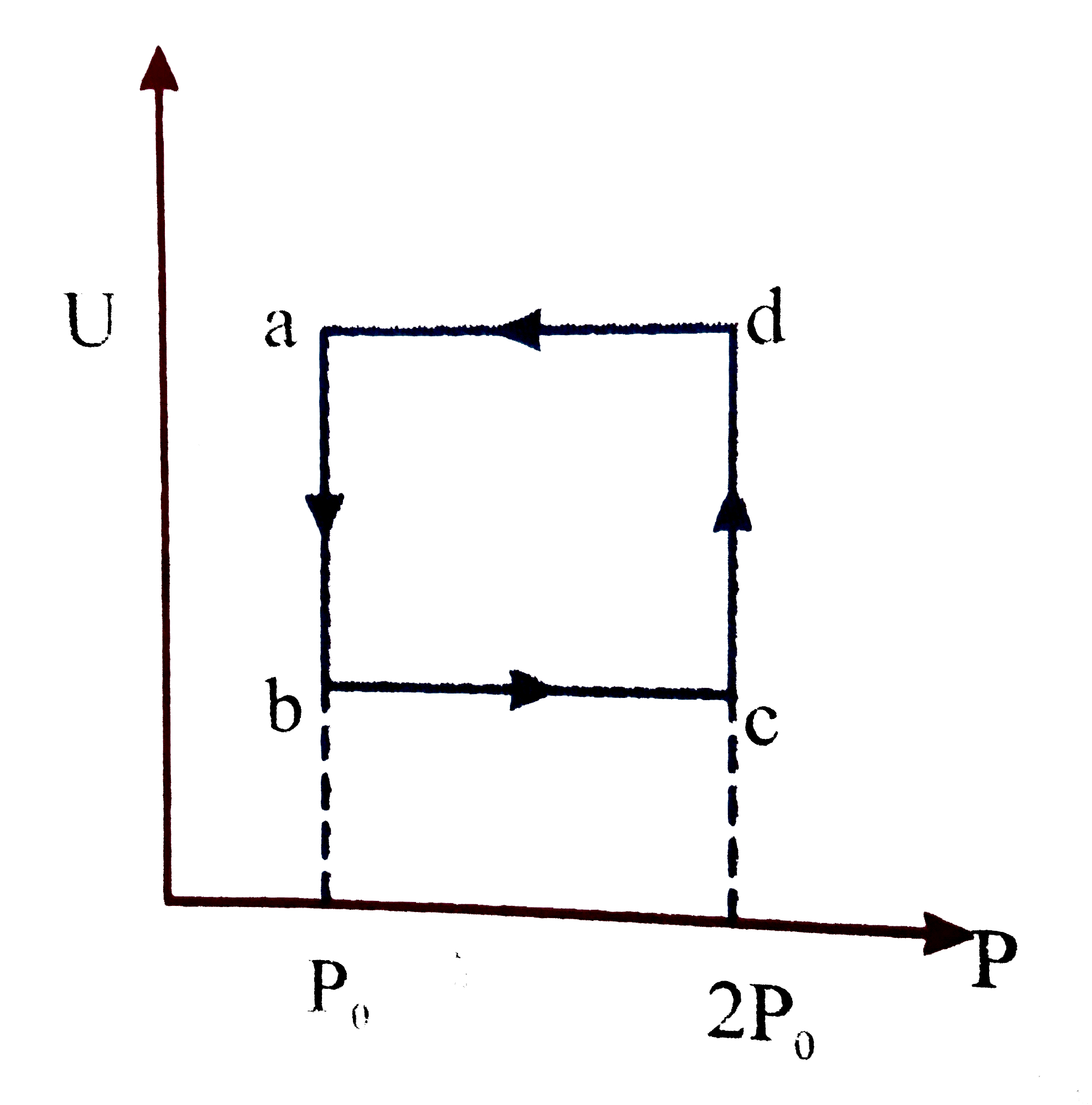
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionIf a gas absorbs 200J of heat and expands by 500cm3 against a constant pressure of 2×105Nm−2, then the change in internal energy is
View Solution
