Two moles of a diatomic ideal gas is taken through pT= constant. Its temperature is increased from T to 2T. Find the work done by the system?
The correct Answer is:D
To find the work done by the system when two moles of a diatomic ideal gas are taken through a process where P⋅T=constant and the temperature is increased from T to 2T, we can follow these steps:
Step 1: Understand the process
We are given that P⋅T=k (a constant). This means that the product of pressure P and temperature T remains constant throughout the process.
Step 2: Relate pressure, volume, and temperature
Using the ideal gas law, we know:
PV=nRT
From this, we can express pressure P as:
P=nRTV
Step 3: Substitute for P
Since P⋅T=k, we can write:
P=kT
Step 4: Differentiate the equation
We know that:
P=kT⟹V=nRTP
Substituting for P:
V=nRT2k
Differentiating this equation with respect to T:
dV=d(nRT2/k)dT=2nRTkdT
Step 5: Set up the work integral
The work done W by the gas during the process is given by:
W=∫PdV
Substituting P and dV:
W=∫kT⋅(2nRTkdT)
This simplifies to:
W=2nR∫dT
Step 6: Evaluate the integral
The limits of integration are from T to 2T:
W=2nR(T)2TT=2nR(2T−T)=2nRT
Step 7: Substitute the number of moles
Given n=2 (two moles of gas):
W=2⋅2RT=4RT
Final Answer
Thus, the work done by the system is:
4RT
---
We are given that P⋅T=k (a constant). This means that the product of pressure P and temperature T remains constant throughout the process.
Using the ideal gas law, we know:
PV=nRT
From this, we can express pressure P as:
P=nRTV
Since P⋅T=k, we can write:
P=kT
We know that:
P=kT⟹V=nRTP
Substituting for P:
V=nRT2k
Differentiating this equation with respect to T:
dV=d(nRT2/k)dT=2nRTkdT
The work done W by the gas during the process is given by:
W=∫PdV
Substituting P and dV:
W=∫kT⋅(2nRTkdT)
This simplifies to:
W=2nR∫dT
The limits of integration are from T to 2T:
W=2nR(T)2TT=2nR(2T−T)=2nRT
Given n=2 (two moles of gas):
W=2⋅2RT=4RT
Thus, the work done by the system is:
4RT
Topper's Solved these Questions
Similar Questions
In a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionTwo moles of an ideal monatomic gas is heated at constant pressure so that its temperature increases from 127∘C to 227∘C , then work done by gas
View SolutionTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the p - T diagram. During the process AB, the pressure and temperature of the gas vary such that pT = constant. If T1=300K and the amount of heat released by the gas during the process AB is Q=−xR, then the value of x is
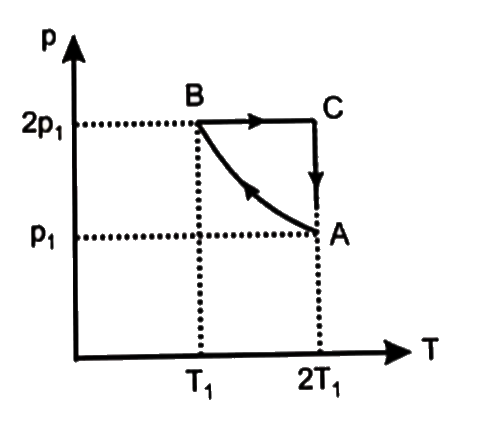
View Solution
