A uniform disc of radius R is pivoted at point O on its circumstances. The time period of small oscillations about an axis passing through O and perpendicular to plane of disc will be
The correct Answer is:D
To solve the problem of finding the time period of small oscillations of a uniform disc pivoted at a point on its circumference, we can follow these steps:
Step 1: Understand the System
We have a uniform disc of radius R and mass M that is pivoted at point O on its circumference. We need to find the time period of small oscillations about an axis passing through O and perpendicular to the plane of the disc.
Step 2: Use the Formula for Time Period of a Physical Pendulum
The time period T of a physical pendulum is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the disc,
- g is the acceleration due to gravity,
- d is the distance from the pivot point to the center of mass of the disc.
Step 3: Calculate the Moment of Inertia
To find the moment of inertia I about point O, we can use the parallel axis theorem:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass (which is at the center of the disc) and d is the distance from the center of mass to the pivot point.
For a disc, the moment of inertia about the center is:
Icm=12MR2
The distance d from the pivot point O to the center of the disc (which is at a distance R from O) is R.
Thus, we can substitute into the parallel axis theorem:
I=12MR2+M(R2)=12MR2+MR2=32MR2
Step 4: Calculate the Distance d
The distance d from the pivot point O to the center of mass of the disc is simply the radius R.
Step 5: Substitute into the Time Period Formula
Now we can substitute I and d into the time period formula:
T=2π
⎷32MR2MgR
Here, the mass M cancels out:
T=2π
⎷32R2gR=2π√3R2g
Step 6: Final Result
Thus, the time period of small oscillations is:
T=2π√3R2g
We have a uniform disc of radius R and mass M that is pivoted at point O on its circumference. We need to find the time period of small oscillations about an axis passing through O and perpendicular to the plane of the disc.
The time period T of a physical pendulum is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the disc,
- g is the acceleration due to gravity,
- d is the distance from the pivot point to the center of mass of the disc.
To find the moment of inertia I about point O, we can use the parallel axis theorem:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass (which is at the center of the disc) and d is the distance from the center of mass to the pivot point.
Icm=12MR2
The distance d from the pivot point O to the center of the disc (which is at a distance R from O) is R.
I=12MR2+M(R2)=12MR2+MR2=32MR2
The distance d from the pivot point O to the center of mass of the disc is simply the radius R.
Now we can substitute I and d into the time period formula:
T=2π
⎷32MR2MgR
Here, the mass M cancels out:
T=2π
⎷32R2gR=2π√3R2g
Thus, the time period of small oscillations is:
T=2π√3R2g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
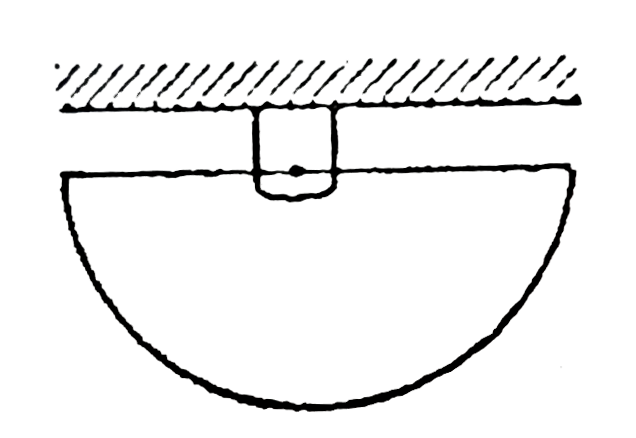
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionFrom a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is

View SolutionFrom a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is

View SolutionA uniform brass disc of radius a and mass m is set into spinning with angular speed ω0 about an axis passing through centre of disc and perpendicular to the palne of disc. If its temperature increases from θ∘1C to θ∘2C with out disturbing the disc, what will be its new angular speed ?
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View Solution
