Let T1 and T2 be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
T=T1+T2
T=T1T2T1+T2
T2=T21+T22
1T2=1T21+1T22
The correct Answer is:D
To solve the problem, we need to establish a relationship between the time periods T1, T2, and T when two springs are connected in parallel. Here’s a step-by-step solution:
Step 1: Understand the Time Period of a Spring
The time period T of a mass m suspended from a spring with spring constant k is given by the formula:
T=2π√mk
Step 2: Write the Time Periods for Each Spring
For spring A with spring constant kA:
T1=2π√mkA
For spring B with spring constant kB:
T2=2π√mkB
Step 3: Combine the Springs in Parallel
When springs A and B are connected in parallel, the equivalent spring constant keq is the sum of the individual spring constants:
keq=kA+kB
Step 4: Write the Time Period for the Combined Springs
The time period T for the combined system is given by:
T=2π√mkeq=2π√mkA+kB
Step 5: Square the Time Period Equations
Now, we will square the equations for T1, T2, and T:
T21=4π2mkA
T22=4π2mkB
T2=4π2mkA+kB
Step 6: Take the Reciprocals
Taking the reciprocal of each squared time period:
1T21=kA4π2m
1T22=kB4π2m
1T2=kA+kB4π2m
Step 7: Add the Reciprocals of T21 and T22
Adding the reciprocals of T21 and T22:
1T21+1T22=kA4π2m+kB4π2m=kA+kB4π2m
Step 8: Relate to the Time Period T
From the equation for T:
1T2=kA+kB4π2m
Thus, we can conclude:
1T2=1T21+1T22
Final Result
This leads us to the final relationship:
1T2=1T21+1T22
Conclusion
The correct answer is:
Option 4: 1T2=1T21+1T22
---
The time period T of a mass m suspended from a spring with spring constant k is given by the formula:
T=2π√mk
For spring A with spring constant kA:
T1=2π√mkA
For spring B with spring constant kB:
T2=2π√mkB
When springs A and B are connected in parallel, the equivalent spring constant keq is the sum of the individual spring constants:
keq=kA+kB
The time period T for the combined system is given by:
T=2π√mkeq=2π√mkA+kB
Now, we will square the equations for T1, T2, and T:
T21=4π2mkA
T22=4π2mkB
T2=4π2mkA+kB
Taking the reciprocal of each squared time period:
1T21=kA4π2m
1T22=kB4π2m
1T2=kA+kB4π2m
Adding the reciprocals of T21 and T22:
1T21+1T22=kA4π2m+kB4π2m=kA+kB4π2m
From the equation for T:
1T2=kA+kB4π2m
Thus, we can conclude:
1T2=1T21+1T22
This leads us to the final relationship:
1T2=1T21+1T22
The correct answer is:
Option 4: 1T2=1T21+1T22
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Let T1andT2 be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass M is, suspended from the séries combination, the time period is T, then
View SolutionA body of mass m has time period T1 with one spring and has time period T2 with another spring. If both the springs are connected in parallel and same mass is used, then new time period T is given as
View SolutionThe time period of a spring mass system of spring constant k and mass m is T. Now, the spring is cut into two equal parts and connected in parallel. If the same mass is attached to new arrangement, then new time period is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionThe time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
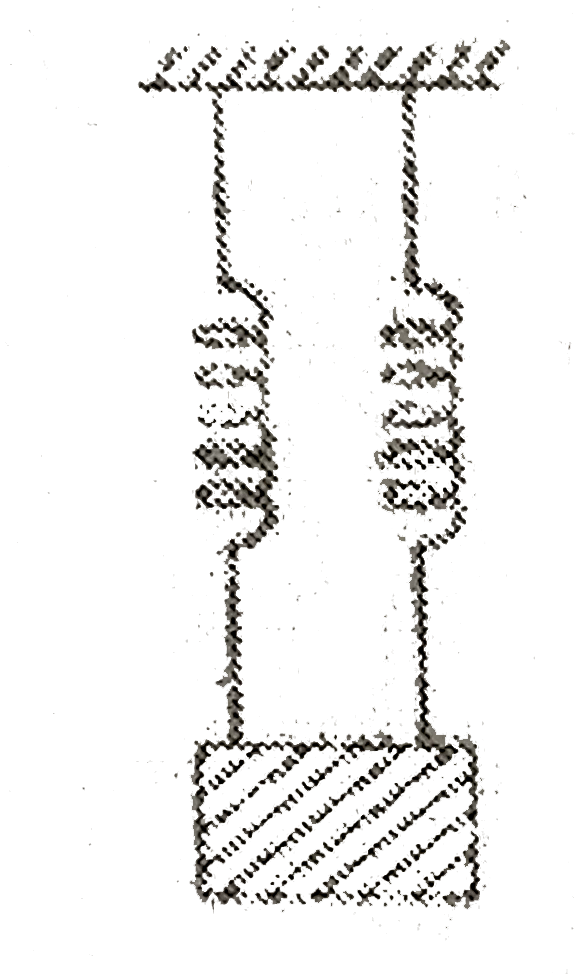
View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View Solution
