Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
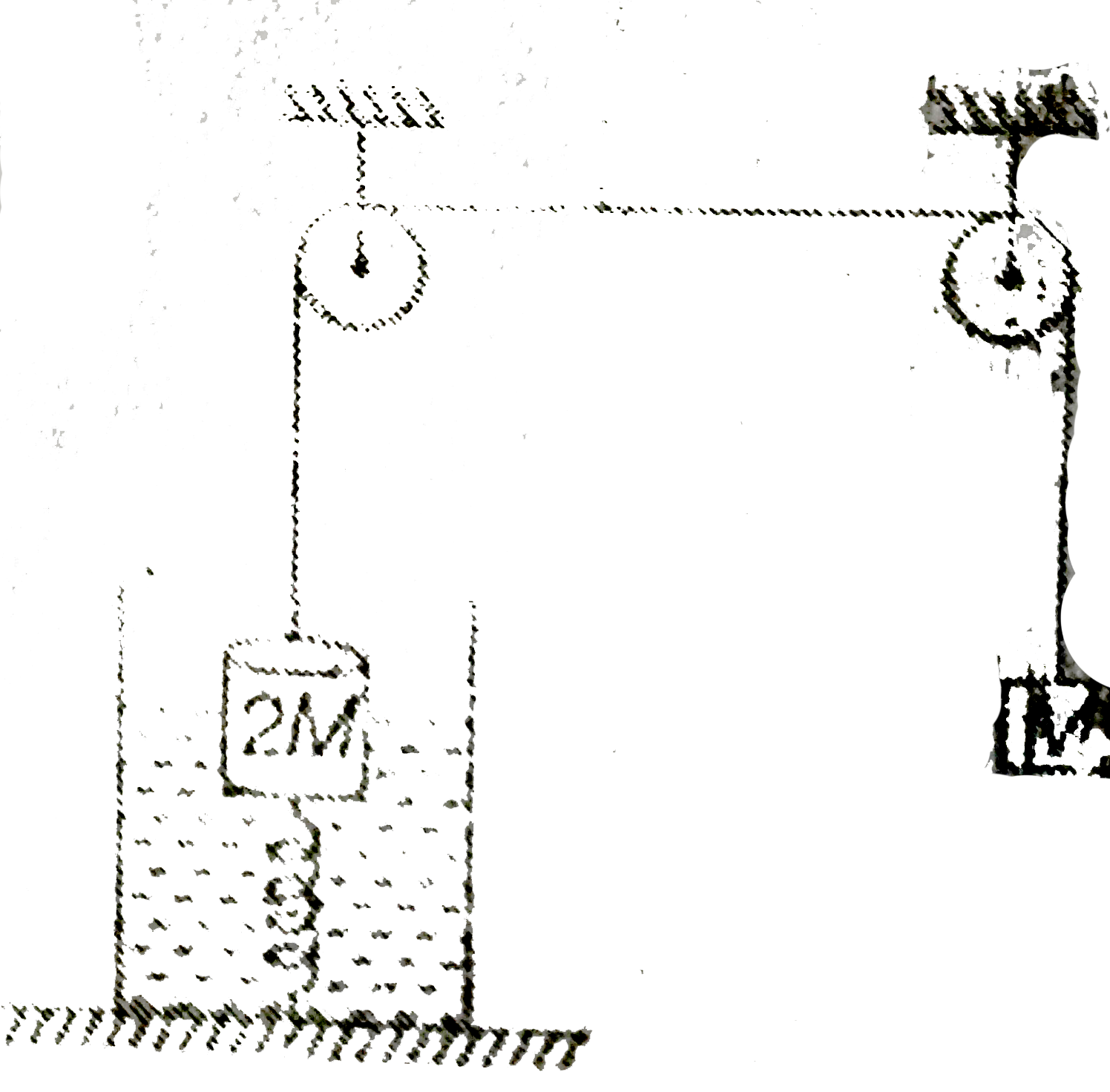
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.
(2pisqrt((3M)/(2(K+Arhog)
(2π√M2K+Aρg
2π√3MK+Aρg
2π√2MK+3Aρg
The correct Answer is:C
Step by step video & image solution for Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density rho, density of the material of the cylinder is 3rho. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed) If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Passage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is
View SolutionIn SHM, match the following.

View SolutionA particle moves such that its acceleration is given by a=−β(x−2)
Here, β is a positive constnt and x the x-coordinate with respect to the origin. Time period of oscillation is
View SolutionWhen an electric field is applied across a semiconductor,
View SolutionIf a machine perform 4000 J output work and 1000 J is inside loss due to friction , then the find efficiency?
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View Solution
Cylindrical block of area of cross-section A and of material of density ρ is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of te length of the block. if acceleration due to gravity is g, the spring constant of the spring is
View SolutionA uniform cylindrical block of length l density d_(1) and area of cross section A floats in a liquid of density d_(2) contained in a vessel (d_(2) gt d_(1)) . The bottom of the cylinder just rests on a spring of contant k. The other end of the spring is fixed to the bottom of the vessel. A weight that may be placed on top of the cylinder such that the cylinder is just submerged in the liquid. find the weight.
View SolutionA cubical block 'A' of mass m_(0)(=a^(3)rho=3 kg) of edge 'a' and density rho floats in a liquid of density 3rho . The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a^(2)rho g) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
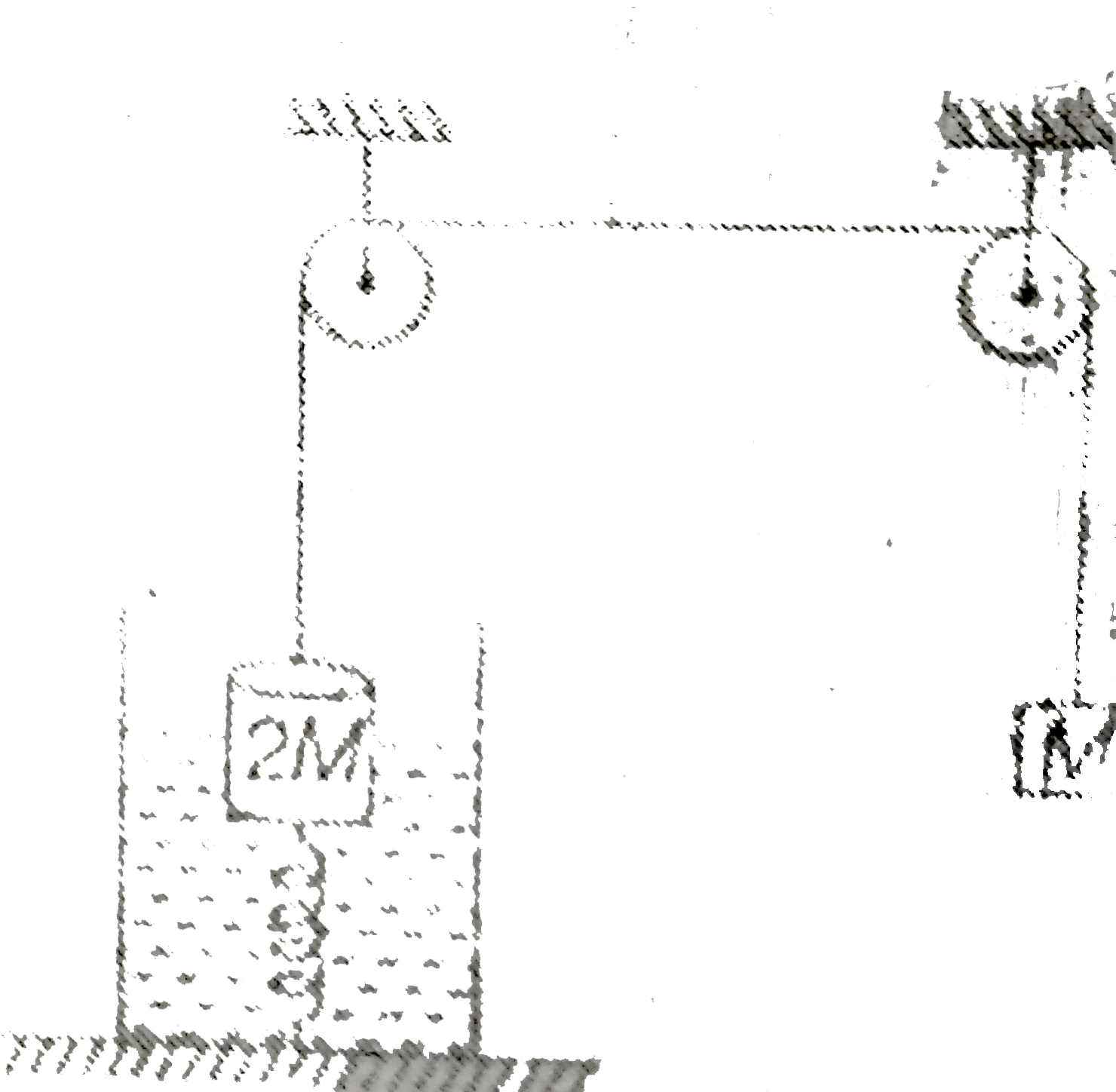
Under equilibrium conditions
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
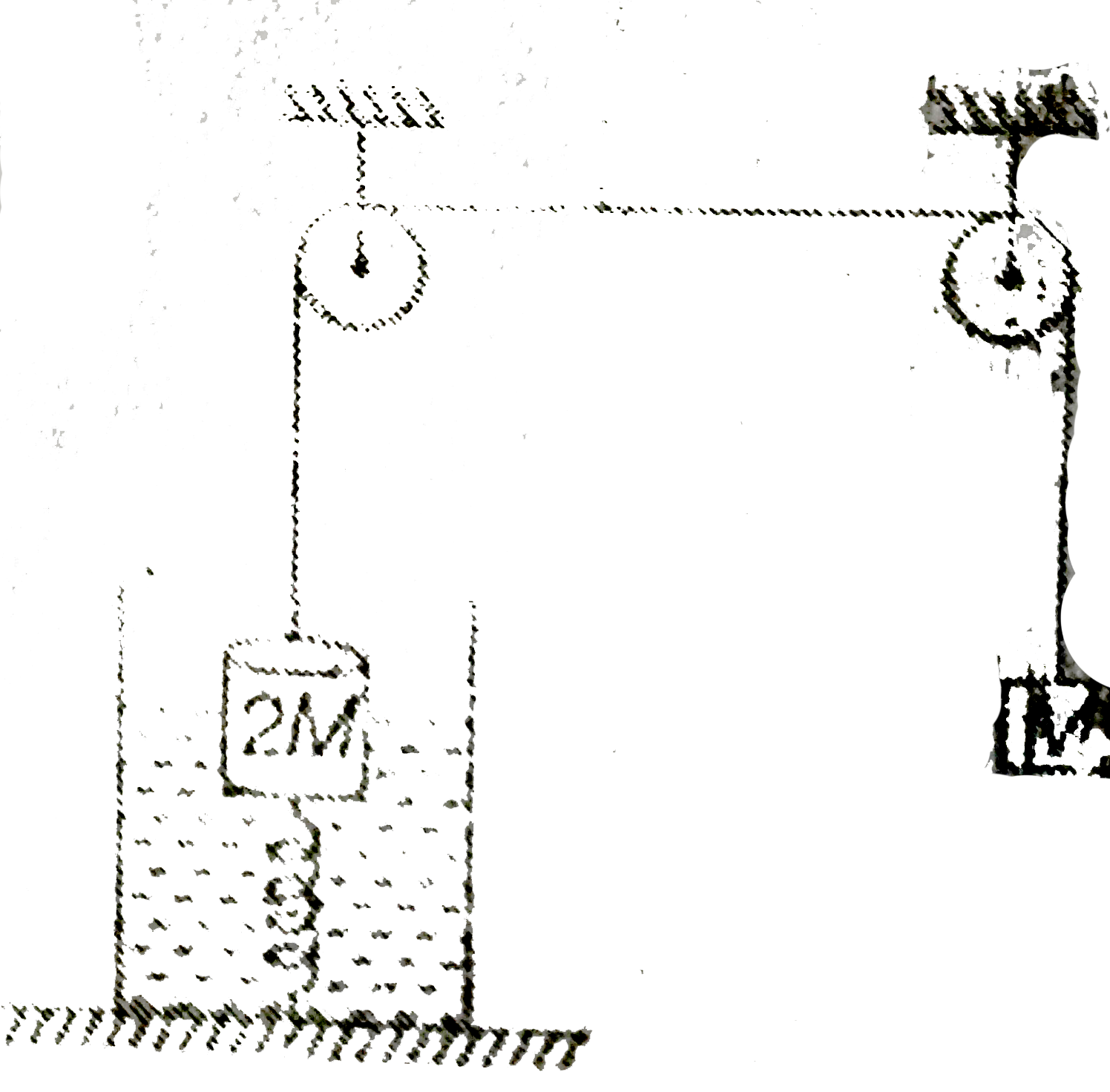
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.
View SolutionA uniform cylinder of length L and mass M having cross sectional area A is suspended , with its length vertical, from a fixed point by a massless spring of spring constant k,such that it is half submerged in a liquid of density sigma at equilibrium position. What is the extension of the spring when it is in equilibrium?
View SolutionTwo blocks, of masses M and 2M are connected to a light spring of spring constant K that has one end fixed, a shown if fig. The blocks are released from the spring at its natural length codition.
View SolutionFigure shows a solid uniform cylinder of radius R and mass M , which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A . Distance OA is equal to (R)/(2) . An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density rho . If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.
View Solution
