The ratio of is maximum I s
2
The correct Answer is:B
To solve the problem, we need to analyze the decay process of the nuclei A, B, and C. The decay constants are given as follows:
- A decays to B with a decay constant λ.
- B decays to C with a decay constant 2λ.
At time T=0:
- The number of nuclei of A, N0=N(0).
- The number of nuclei of B and C, N1=0 and N2=0.
We need to find the ratio N1N2 when N2 is at its maximum.
1. Write the differential equations for the decay process:
- The rate of change of N1 (number of nuclei of B) is given by:
dN1dt=λN0−λN1
- The rate of change of N2 (number of nuclei of C) is given by:
dN2dt=λN1−2λN2
2. Set the condition for maximum N2:
- For N2 to be at a maximum, the rate of change must be zero:
dN2dt=0
- Therefore, we have:
λN1−2λN2=0
- This simplifies to:
N1=2N2
3. Find the ratio N1N2:
- From the equation N1=2N2, we can express the ratio:
N1N2=2
4. Conclusion:
- The ratio N1N2 when N2 is maximum is 2.
Final Answer:
N1N2=2
- B decays to C with a decay constant 2λ.
- The number of nuclei of A, N0=N(0).
- The number of nuclei of B and C, N1=0 and N2=0.
- The rate of change of N1 (number of nuclei of B) is given by:
dN1dt=λN0−λN1
- The rate of change of N2 (number of nuclei of C) is given by:
dN2dt=λN1−2λN2
- For N2 to be at a maximum, the rate of change must be zero:
dN2dt=0
- Therefore, we have:
λN1−2λN2=0
- This simplifies to:
N1=2N2
- From the equation N1=2N2, we can express the ratio:
N1N2=2
- The ratio N1N2 when N2 is maximum is 2.
N1N2=2
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (only one option is Correct)
76 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
Aλ−−→B2λ−−→C
T=0,N0,0,
TN1N2N3
The ratio of N1 to N2 is maximum I s
View SolutionAλ1−−→Bλ2−−→C
t=0 N0 0 0
tN1N2N3 In the above radioactive decay C is stable nucleus. Then:
View SolutionN2O3R.T.−−→NO+NO2
View SolutionN2O3R.T.−−→NO+NO2
View SolutionThe reaction
.1D2+.1T3→.1He2+.0n1
is an example of
View SolutionBaC2+N2Δ−−→(A)CaC2+N2Δ−−→(B)
(A) and (B) are
View SolutionIf (12−t1)+(22−t2)+......+(n2−tn)=13n(n2−1), then tn is
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The net rate of accumulation of B at any instant is
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
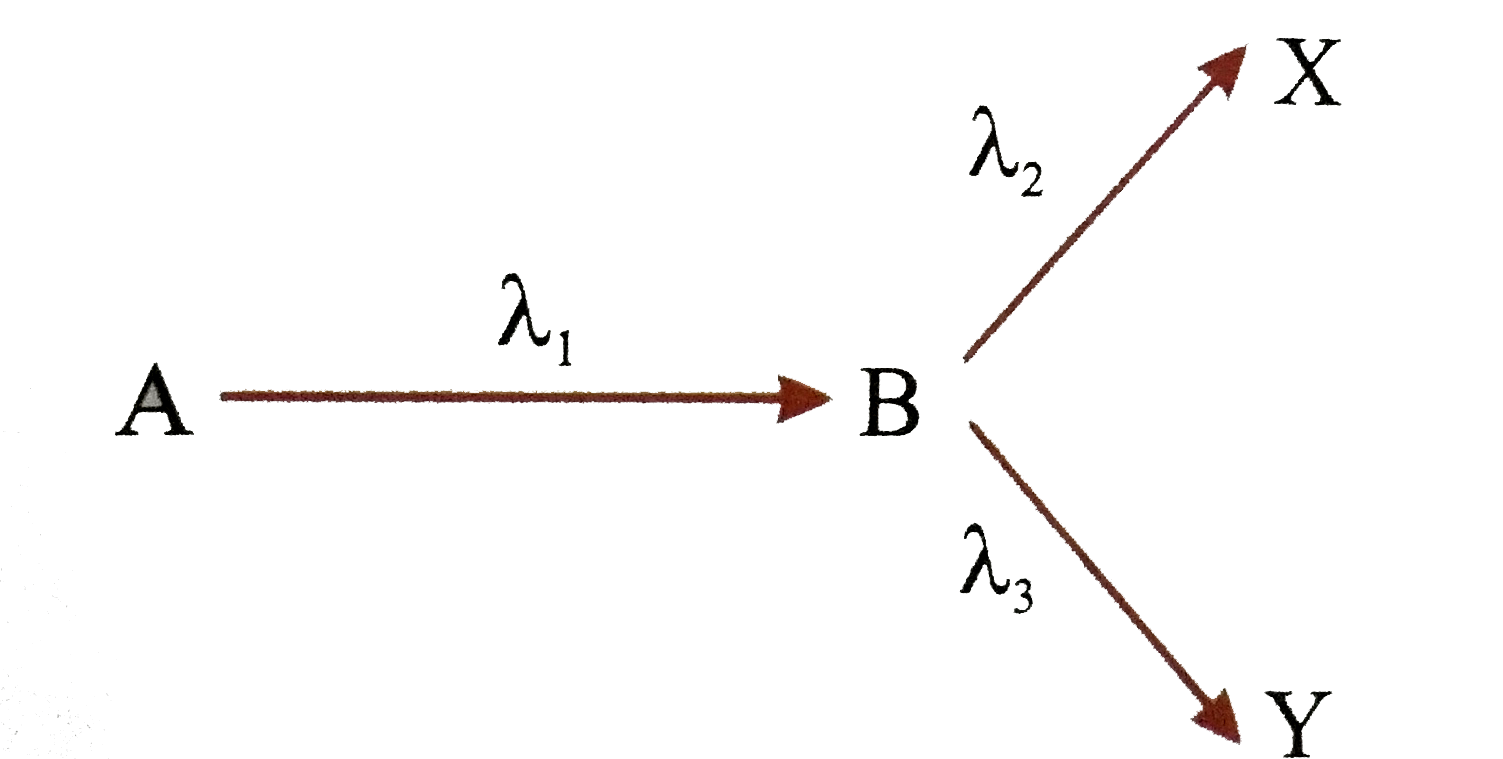
The number of nuclei of B will first increase and then after a maximum value, it decreases for
View SolutionThe first two terms of a sequence are 0 and 1, The nth terms Tn=2Tn−1−Tn−2,n≥3. For example the third terms T3=2T2−T1=2−0=2, The sum of the first 2006 terms of this sequence is :
View Solution
