Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
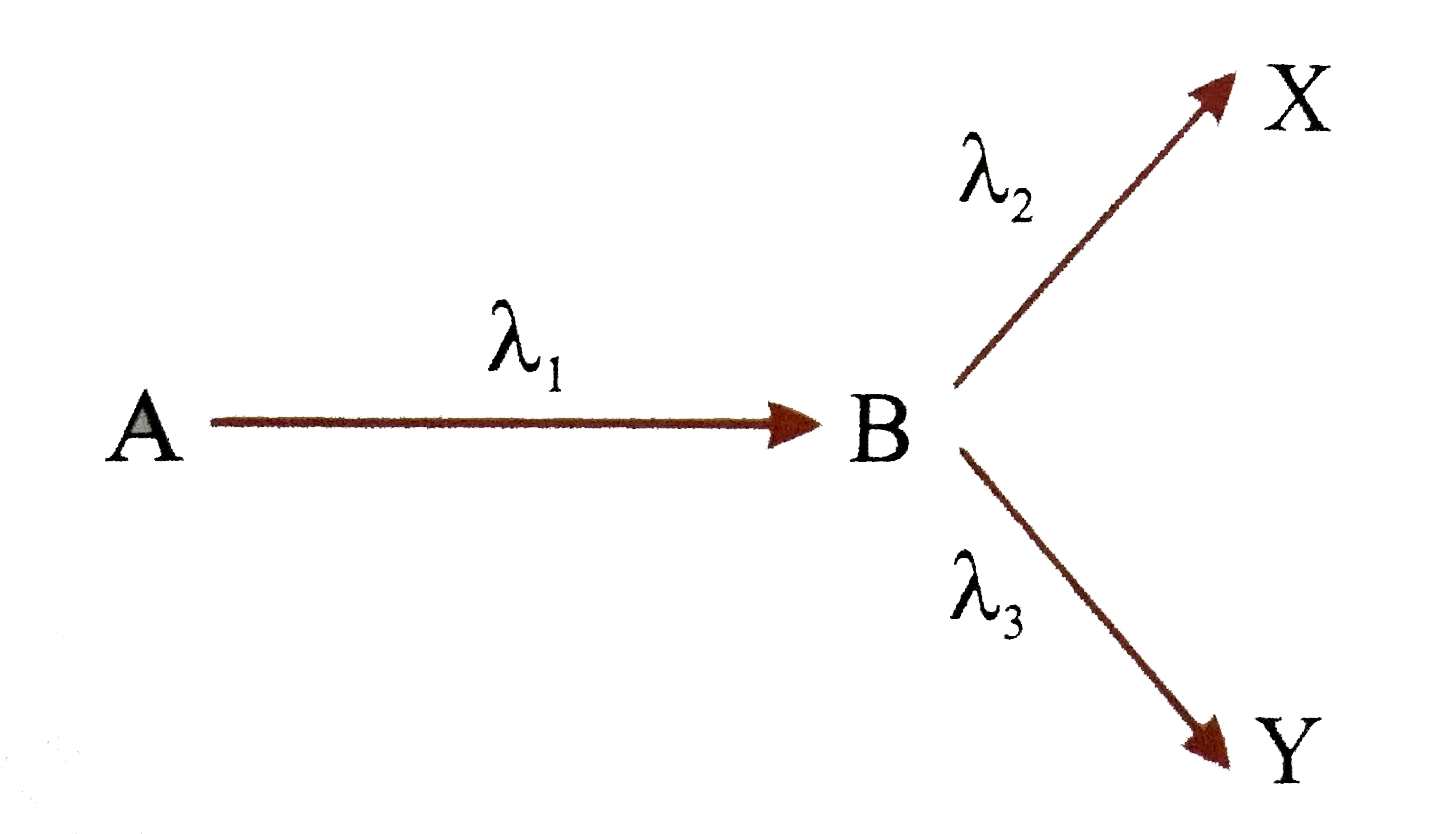
The net rate of accumulation of B at any instant is
N1λ1+N2λ2+N3λ3
N1λ1−N3λ2−N4λ3
N1λ1−N2λ2−N2λ3
N1λ1+N2λ2−N3λ3
The correct Answer is:C
Rate of production of B depends on the decaying rate (A) : dNAdt=−λNA=λN1
B is decaying simultaneously with two rates dNBdt=−λ2NB=−λ2N2
dNBdt=−λ3NB=−λ3N2
Number of nuclei of 'B' is =λ1N1−λ2N2−λ3N2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 372videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 382videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 352videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
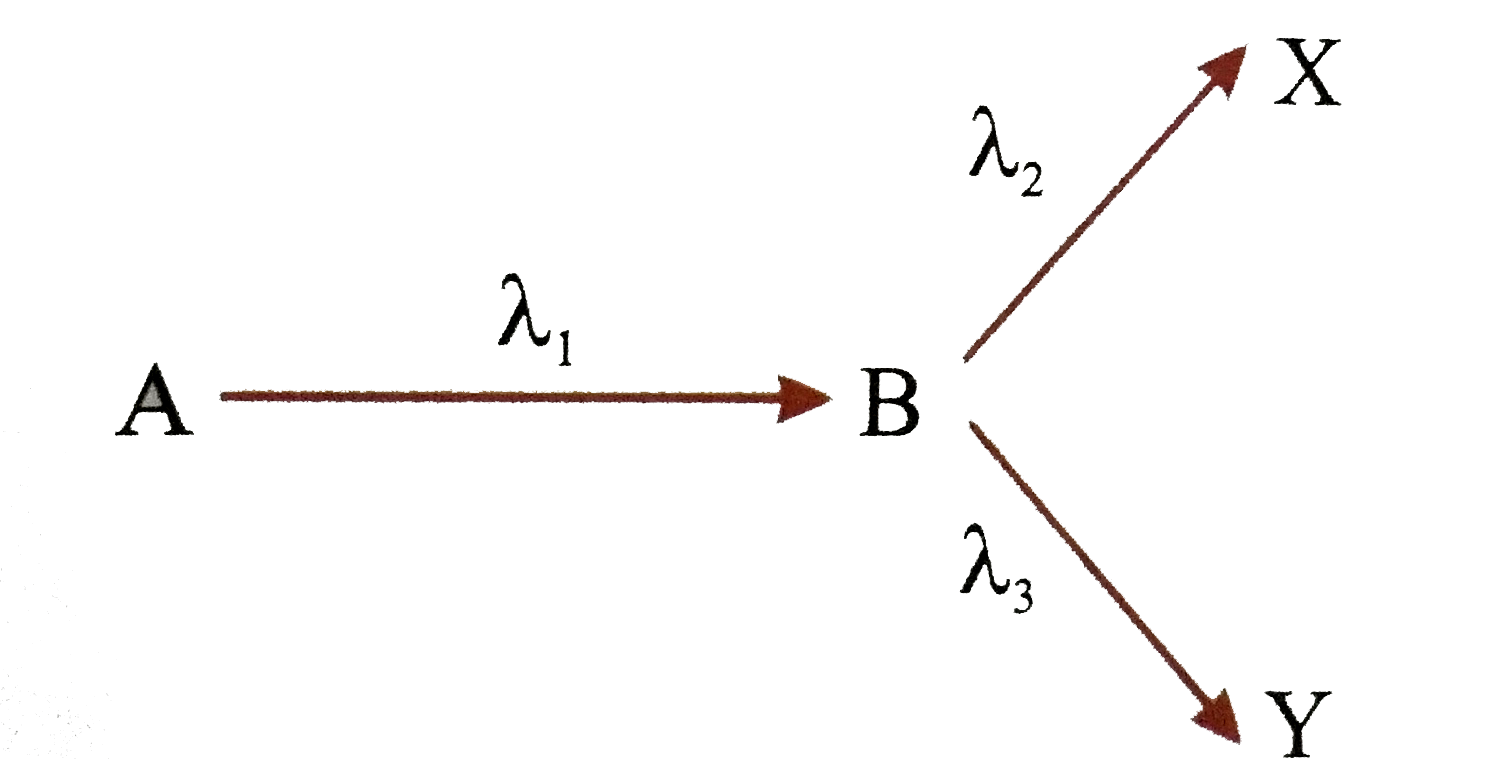
The number of nuclei of B will first increase and then after a maximum value, it decreases forView SolutionReplum is present in the ovary of flowers of
View SolutionThe rate of biomass production by consumers is called :
View SolutionTwo radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionNucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
View SolutionIn a decay process A decays to B. A→B. Two graphs of number of nuclei of A and B versus time is given then
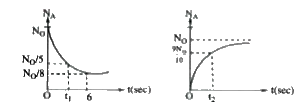 View Solution
View SolutionThe decay constant (λ) for radioactive decay is independent of
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionConsider a radioactive disintegration according to the equation A→B→C. Decay constant of A and B is same and equal to λ. Number of nuclei of A, B and C are N0 , 0, 0 respectively at t=0. Find
(a) number of nuclei of B as function of time t.
(b) time t at which the activity of B is maximum and the value of maximum activity of B.View Solution

