Let be the area enclosed by the orbit in a hydrogen atom. The graph of against In
will pass through origin
will be a straight line with slope 4
will be a parabola
will be a circle
The correct Answer is:A, B
To solve the problem, we need to analyze the area enclosed by the nth orbit in a hydrogen atom and how it relates to the quantum number n.
Step 1: Understanding the Radius of the nth Orbit
The radius of the nth orbit in a hydrogen atom is given by the formula:
rn=r0n2
where r0 is a constant.
Step 2: Calculating the Area of the nth Orbit
The area An enclosed by the nth orbit can be calculated using the formula for the area of a circle:
An=πr2n
Substituting the expression for rn:
An=π(r0n2)2=πr20n4
Step 3: Expressing the Area in Terms of a Reference Area
Let’s denote the area of the first orbit as A1:
A1=πr20(14)=πr20
Now, we can express the area An in terms of A1:
An=A1n4
Step 4: Taking the Ratio of Areas
Now, we can take the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=n4
Step 5: Taking the Natural Logarithm
Taking the natural logarithm of both sides gives:
ln(AnA1)=ln(n4)
Using the properties of logarithms, we can simplify this to:
ln(AnA1)=4ln(n)
Step 6: Rearranging the Equation
Rearranging the equation, we can express it as:
ln(An)−ln(A1)=4ln(n)
This indicates that if we plot ln(An) against ln(n), we will get a straight line with a slope of 4.
Step 7: Analyzing the Graph
The graph of ln(AnA1) against ln(n) will be a straight line passing through the origin with a slope of 4.
Conclusion
Thus, the graph of ln(AnA1) against ln(n) is a straight line with a slope of 4.
The radius of the nth orbit in a hydrogen atom is given by the formula:
rn=r0n2
where r0 is a constant.
The area An enclosed by the nth orbit can be calculated using the formula for the area of a circle:
An=πr2n
Substituting the expression for rn:
An=π(r0n2)2=πr20n4
Let’s denote the area of the first orbit as A1:
A1=πr20(14)=πr20
Now, we can express the area An in terms of A1:
An=A1n4
Now, we can take the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=n4
Taking the natural logarithm of both sides gives:
ln(AnA1)=ln(n4)
Using the properties of logarithms, we can simplify this to:
ln(AnA1)=4ln(n)
Rearranging the equation, we can express it as:
ln(An)−ln(A1)=4ln(n)
This indicates that if we plot ln(An) against ln(n), we will get a straight line with a slope of 4.
The graph of ln(AnA1) against ln(n) will be a straight line passing through the origin with a slope of 4.
Thus, the graph of ln(AnA1) against ln(n) is a straight line with a slope of 4.
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
Knowledge Check
In a sequence, the nth term an is defined by the rule (an−1−3)2,a1=1 what is the value of a4 ?
A1B4C9D16
The figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
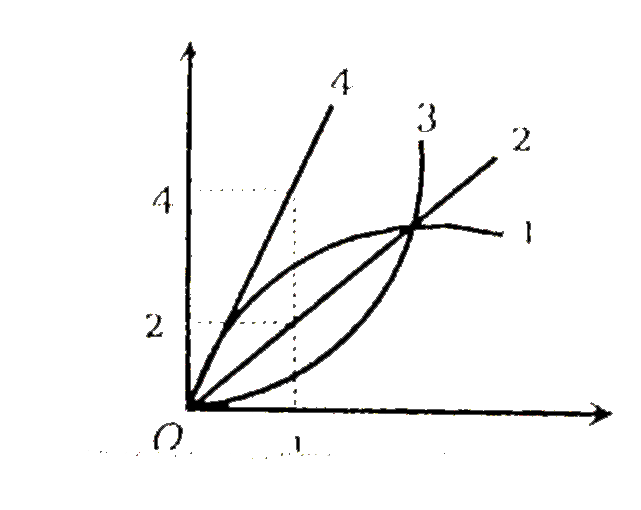
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
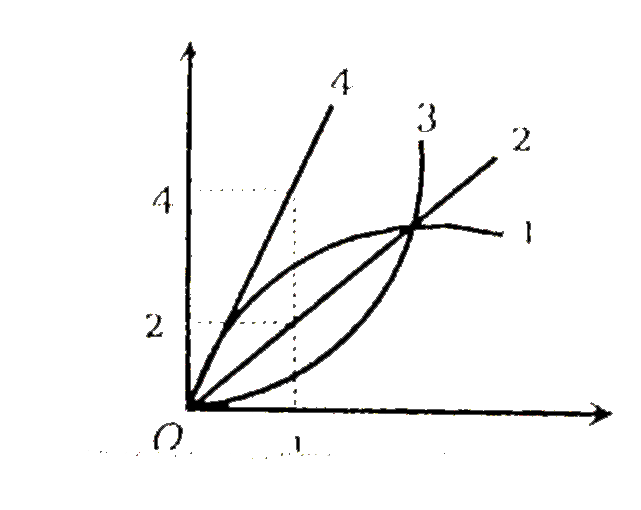
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
View SolutionIf An is the area bounded by y=x and y=xn,n∈N, then A2.A3…An=
View SolutionLet θ=(a1,a2,a3,...,an) be a given arrangement of n distinct objects a1,a2,a3,…,an. A derangement of θ is an arrangment of these n objects in which none of the objects occupies its original position. Let Dn be the number of derangements of the permutations θ.
The relation between Dn and Dn−1 is given by
View SolutionLet A1,A2,A3,…..,An be squares such that for each n≥1 the length of a side of An equals the length of a diagonal of An+1. If the side of A1 be 20 units then the smallest value of 'n' for which area of An is less than 1.
View SolutionLet a1,a2...be positive real numbers in geometric progression. For n, if An,Gn,Hn are respectively the arithmetic mean, geometric mean and harmonic mean of a1,a2,...,an. Then, find an expression for the geometric mean of G1,G2,...,Gn in terms of A1,A2,...,An,H1,H2,...,Hn
View Solution
