What is the range of a projectile thrown with velocity 98m/s with angle 30∘ from horizontal ?
490√3m
245√3m
980√3m
100m
The correct Answer is:A
To find the range of a projectile thrown with an initial velocity of 98m/s at an angle of 30∘ from the horizontal, we can use the formula for the range of a projectile:
R=u2sin2θg
Where:
- R is the range,
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 9.8m/s2).
Step 1: Identify the values
- Initial velocity, u=98m/s
- Angle of projection, θ=30∘
- Acceleration due to gravity, g=9.8m/s2
Step 2: Calculate sin2θ
First, we need to calculate sin2θ:
sin2θ=sin(2×30∘)=sin60∘
From trigonometric values, we know:
sin60∘=√32
Step 3: Plug in the values into the range formula
Now we can substitute the values into the range formula:
R=(98)2⋅sin60∘9.8
R=(98)2⋅√329.8
Step 4: Calculate (98)2
Calculating (98)2:
(98)2=9604
Step 5: Substitute back into the equation
Now substituting back:
R=9604⋅√329.8
R=9604√319.6
Step 6: Simplify the expression
Now, simplifying the expression:
R=490√3meters
Final Answer
Thus, the range of the projectile is:
R=490√3meters
- R is the range,
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 9.8m/s2).
- Initial velocity, u=98m/s
- Angle of projection, θ=30∘
- Acceleration due to gravity, g=9.8m/s2
First, we need to calculate sin2θ:
sin2θ=sin(2×30∘)=sin60∘
From trigonometric values, we know:
sin60∘=√32
Now we can substitute the values into the range formula:
R=(98)2⋅sin60∘9.8
R=(98)2⋅√329.8
Calculating (98)2:
(98)2=9604
Now substituting back:
R=9604⋅√329.8
R=9604√319.6
Now, simplifying the expression:
R=490√3meters
Thus, the range of the projectile is:
R=490√3meters
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
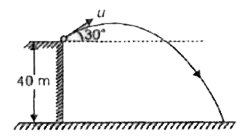
Figure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
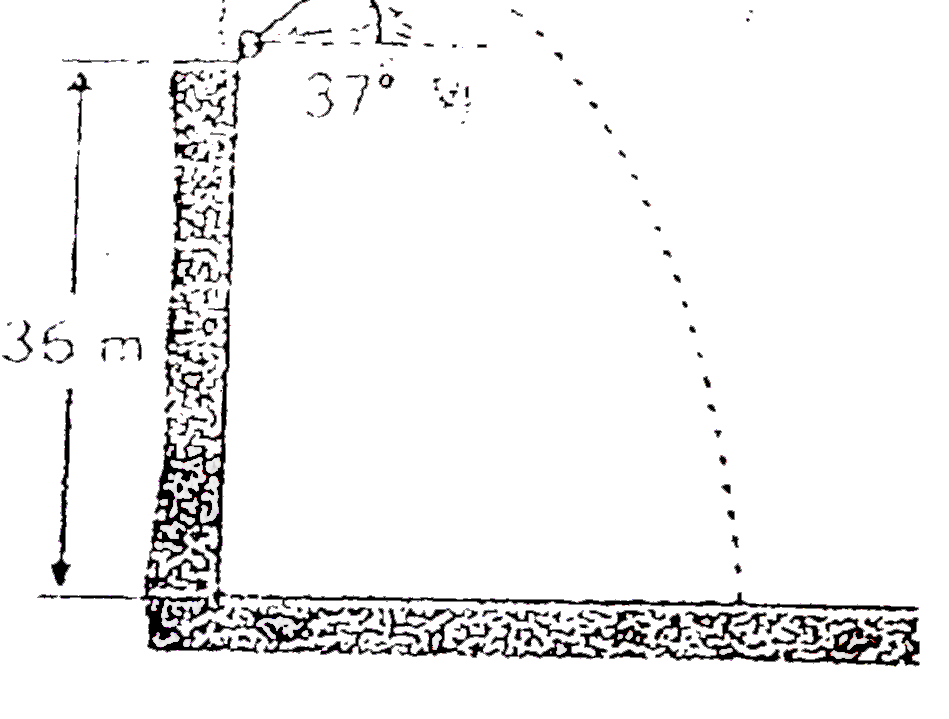 :
:
View Solution
Knowledge Check
The angle which the velocity vector of a projectile thrown with a velocity v at an. angle θ to the horizontal Will make with the horizontal after time t of its being thrown up is
AθBtan−1(θ/t)Ctan−1(vcosθvsinθ−gt)Dtan−1(vsinθ−gtvcosθ)The range of particle when launched at an angle of 15∘ with the horizontal is 1.5 km. What is the range of the projectile when launched at an angle of 45∘ to the horizontal
A1.5 kmB3.0 kmC6.0 kmD0.75 kmIf a body 'A' of mass M is thrown with velocity V at an angle of 30∘ to the horizontal and another body B of the same mass is thrown with the same speed at an angle of 60∘ to the horizontal, the ratio of horizontal ranges of A to B will be
A1:3B1:1C1:√3D√3:1
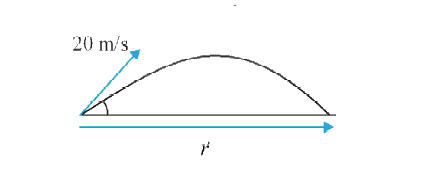
A projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
View SolutionThe range of a projectile, when launched at an angle of 15∘ with the horizontal is 1.5 km. what is the range of the projectile, when launched at an angle of 45∘ to the horizontal with the same speed ?
View SolutionA projectile is thrown from level ground at some angle
View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
View Solution