A body of mass 1 kg executes SHM which is given by
y=6.0cos(100t+π4)cm
What is the maximum kinetic energy ?
3J
6J
9J
18J
The correct Answer is:D
To find the maximum kinetic energy of a body executing simple harmonic motion (SHM) given by the equation y=6.0cos(100t+π4) cm, we can follow these steps:
Step 1: Identify the parameters from the SHM equation
From the equation y=6.0cos(100t+π4):
- The amplitude A is 6.0 cm.
- The angular frequency ω is 100 rad/s.
Step 2: Convert amplitude to meters
Since the amplitude is given in centimeters, we need to convert it to meters:
A=6.0 cm=6.0100 m=0.06 m
Step 3: Use the formula for maximum kinetic energy
The maximum kinetic energy KEmax in SHM can be calculated using the formula:
KEmax=12mω2A2
where:
- m is the mass of the body (1 kg),
- ω is the angular frequency (100 rad/s),
- A is the amplitude (0.06 m).
Step 4: Substitute the values into the formula
Substituting the values into the formula:
KEmax=12×1 kg×(100 rad/s)2×(0.06 m)2
Step 5: Calculate KEmax
Calculating each part:
(100 rad/s)2=10000 rad2/s2
(0.06 m)2=0.0036 m2
Now substituting these back:
KEmax=12×1×10000×0.0036
KEmax=12×36=18 J
Final Answer
The maximum kinetic energy of the body is 18 J.
---
From the equation y=6.0cos(100t+π4):
- The amplitude A is 6.0 cm.
- The angular frequency ω is 100 rad/s.
Since the amplitude is given in centimeters, we need to convert it to meters:
A=6.0 cm=6.0100 m=0.06 m
The maximum kinetic energy KEmax in SHM can be calculated using the formula:
KEmax=12mω2A2
where:
- m is the mass of the body (1 kg),
- ω is the angular frequency (100 rad/s),
- A is the amplitude (0.06 m).
Substituting the values into the formula:
KEmax=12×1 kg×(100 rad/s)2×(0.06 m)2
Calculating each part:
(100 rad/s)2=10000 rad2/s2
(0.06 m)2=0.0036 m2
Now substituting these back:
KEmax=12×1×10000×0.0036
KEmax=12×36=18 J
The maximum kinetic energy of the body is 18 J.
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A body of mass 1 kg is executing simple harmonic motion. Its displacement y(cm) at t seconds is given by y=6sin(100t+π/4) . Its maximum kinetic energy is
View SolutionA body of mass 2 kg is executing simple harmonic motions according to the cquation 0.06 cos (100t+ π/4 ) m, where t is in seconds. What is the maximum kinetic energy?
View SolutionA particle of mass 0.10 kg has its velocity varying according to the relationv=πsin(πt+π4)m/sec
What is the maximum kinetic energy (in joules)?(Takeπ2=10)
View SolutionThe only force acting on a 2.0−kg body as it moves along the x-axis varies as shown in figure. The velocity of the body at x=0 is 4.0ms−1.
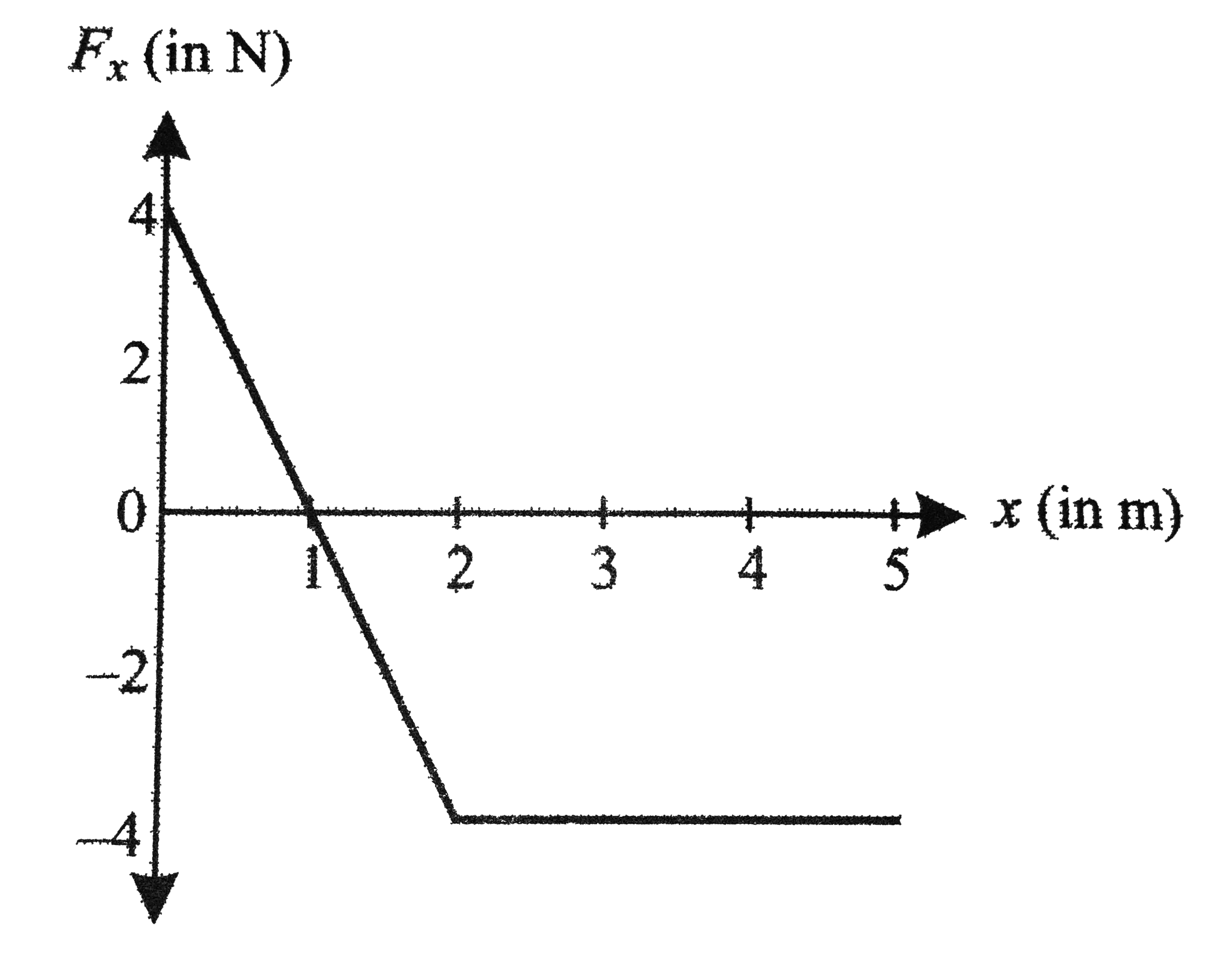
a. What is the kinetic energy of the body at x=3.0m?
b. At what value of x will the body have a kinetic energy of 8.0J?
c. What is the maximum kinetic energy attained by the body between x=0 and x=5.0m?
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionA body of mass 5 kg is thrown vertically up with a kinetic energy of 490 J. What will be height at which the kinetic energy of the body becomes half of the original value ? (Acceleration due to gravity=9.8ms−2)
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionA partical of mass 0.2kg undergoes SHM according to the equation x(t)=3sin(πt+π/4).
i. What is the total energy of the partical if potential energy of zero at mean position ?
ii. What are the kinetic and potential energies of partical at time t=1s?
iii. At what time instants is the particals energies purely kinetic?
View SolutionA body of mass 4 kg is executing shm of amplitude 0.4 m and period 2 s. Find (i) the maximum restoring force and (ii) the restoring force at a distance of 0.1 m from extreme position.
View SolutionA 2.0kg particle undergoes SHM according to x=1.5cos(πt4+π6) (in SI .units)
(a) What is the total mechanical energy of the particle ?
(b) What is the shortest time required for the particle to move from x=0.5m to x=−0.75m ?
View Solution
