The only force acting on a 2.0−kg body as it moves along the x-axis varies as shown in figure. The velocity of the body at x=0 is 4.0ms−1.
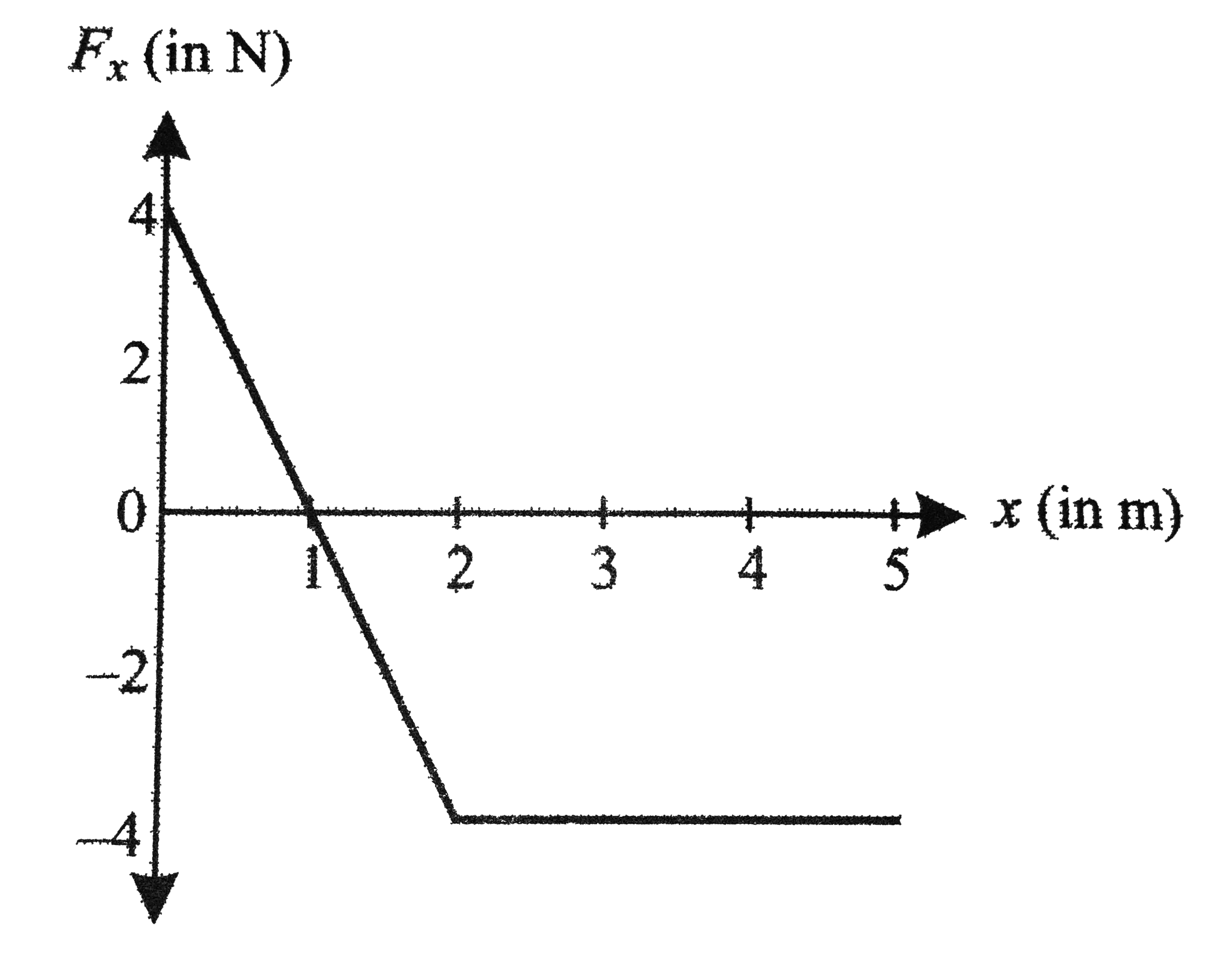
a. What is the kinetic energy of the body at x=3.0m?
b. At what value of x will the body have a kinetic energy of 8.0J?
c. What is the maximum kinetic energy attained by the body between x=0 and x=5.0m?
Kinetic energy of the body at x=0 is
K1=12×2.0×(4.0)2=16.0J
Work done by the force on the body is given by the area bounded by the curve and x-axis in figure. From x=0 to x=1.0m, the force decreases linearly from Fx=4N to 0, but it is directed along positive x-axis. Work done by the force is positive. For 1.0m<x≤5.0m, the force is negative, so it is directed along the negative x-axis for any interval in this region. the work done by the force will be negative.
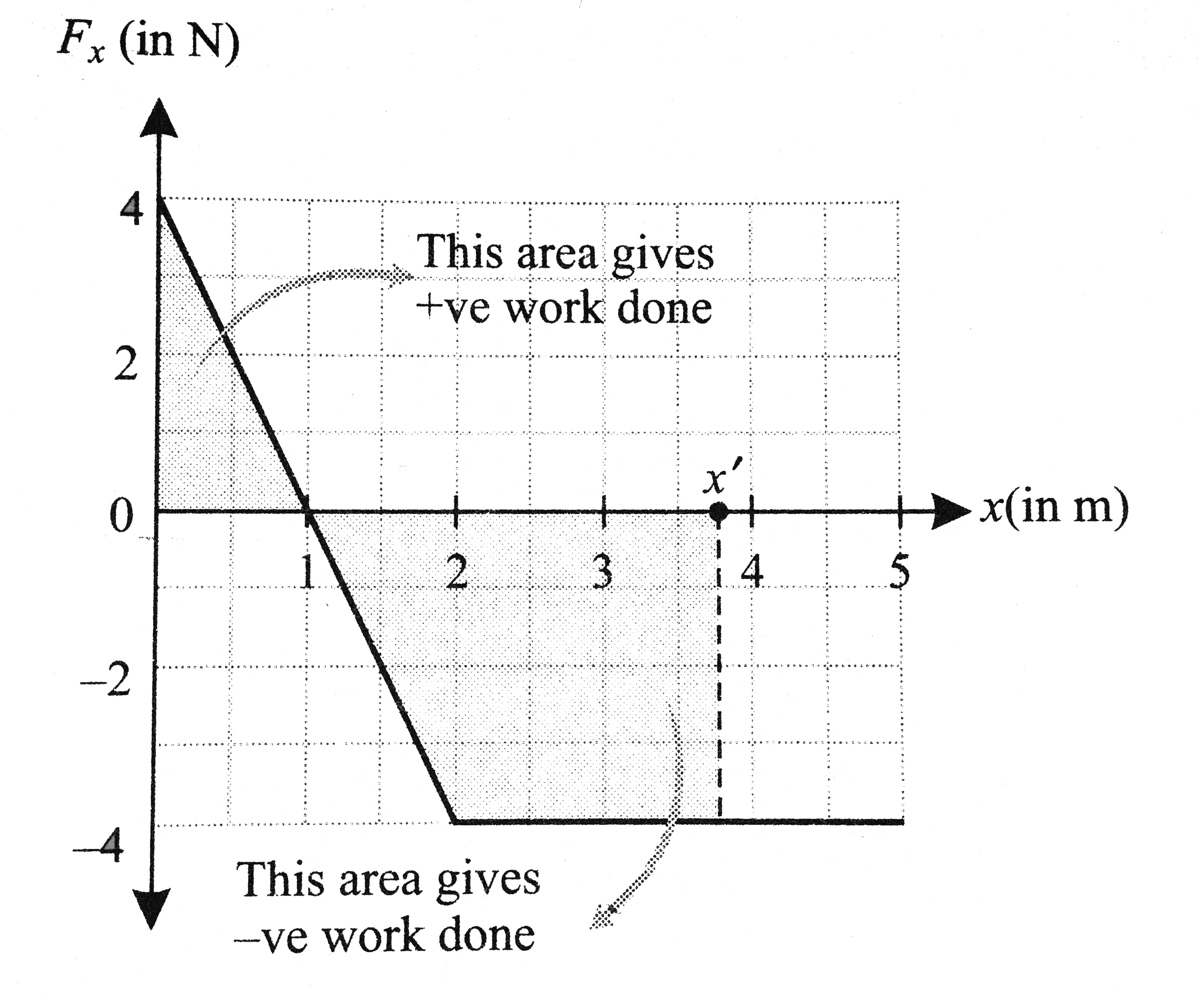
a. From x=0 to 3.0m, work done by the force on the body
=Area of Fx−x diagram between x=0 to x=3.0m region in figure.
12×4×1.0−12×4×1.0−4×1.0=−4.0Nm=−4.0J
Let the kinetic energy of the body at x=3.0m be K3. From the work-energy theorem, W=ΔK.
−4.0=K3−16.0J⇒K3=12.0J
b. Let the kinetic energy of the body be 8.0J at x=x′.
From x=0 to x′, work done by the force=Area of the graph between x=0 to x′ shown in figure, i.e.,
12×4×1.0−12×4×1.0−4×(x′−2.0)Nm=−4×(x′−2.0)J
Using the work-energy theorem, we get
−4×(x′−2.0)=8.0−16.0(∑W=K2−K1)
x′=4.0m
Incidentally, in the diagram, x′ has been drawn between 3.0m and 4.0m. You must not infer from this that x′ lies between 3.0m and 4.0m
c. From x=0 to 5.0m, when the work done by the force is positive, kinetic energy of the block increases. Subsequently, when the work done by the force is negative, kinetic energy of the block decreases. Then, clearly, the kinetic energy of the block is maximum at x=1.0m. Using the work-energy theorem again, we get
12×4×1.0=Kmax−K1
Kmax=K1+2.0=16.0+2.0=18.0J
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
The kinetic energy of a body moving along a straight line varies with time as shown in figure. The force acting on the body:
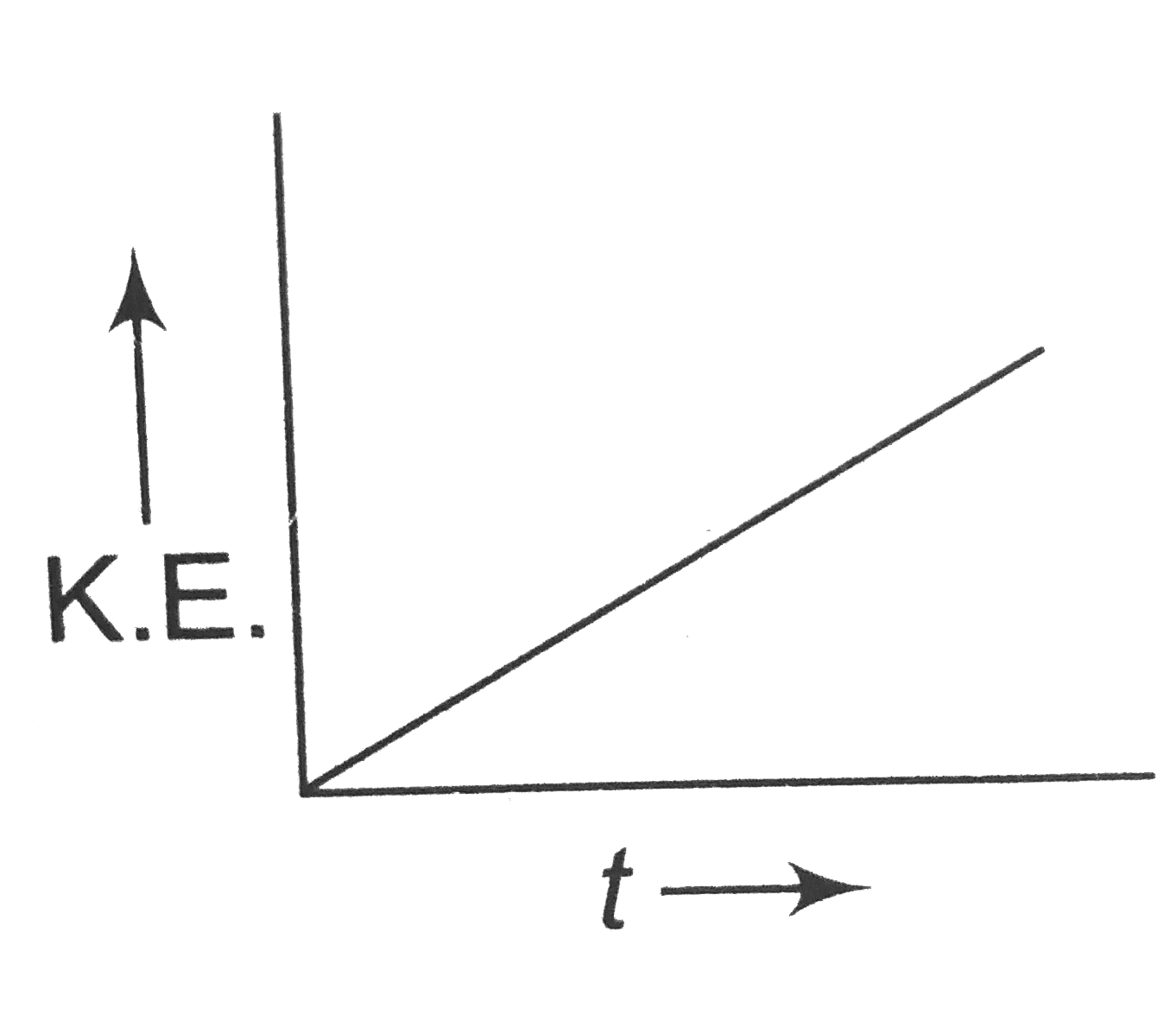 View Solution
View SolutionWhat do you understand by the kinetic energy of a body?
View SolutionThe force acting on a body moving along x-axis variation of the particle particle shown in the figure. The body is in stable equilibrium at
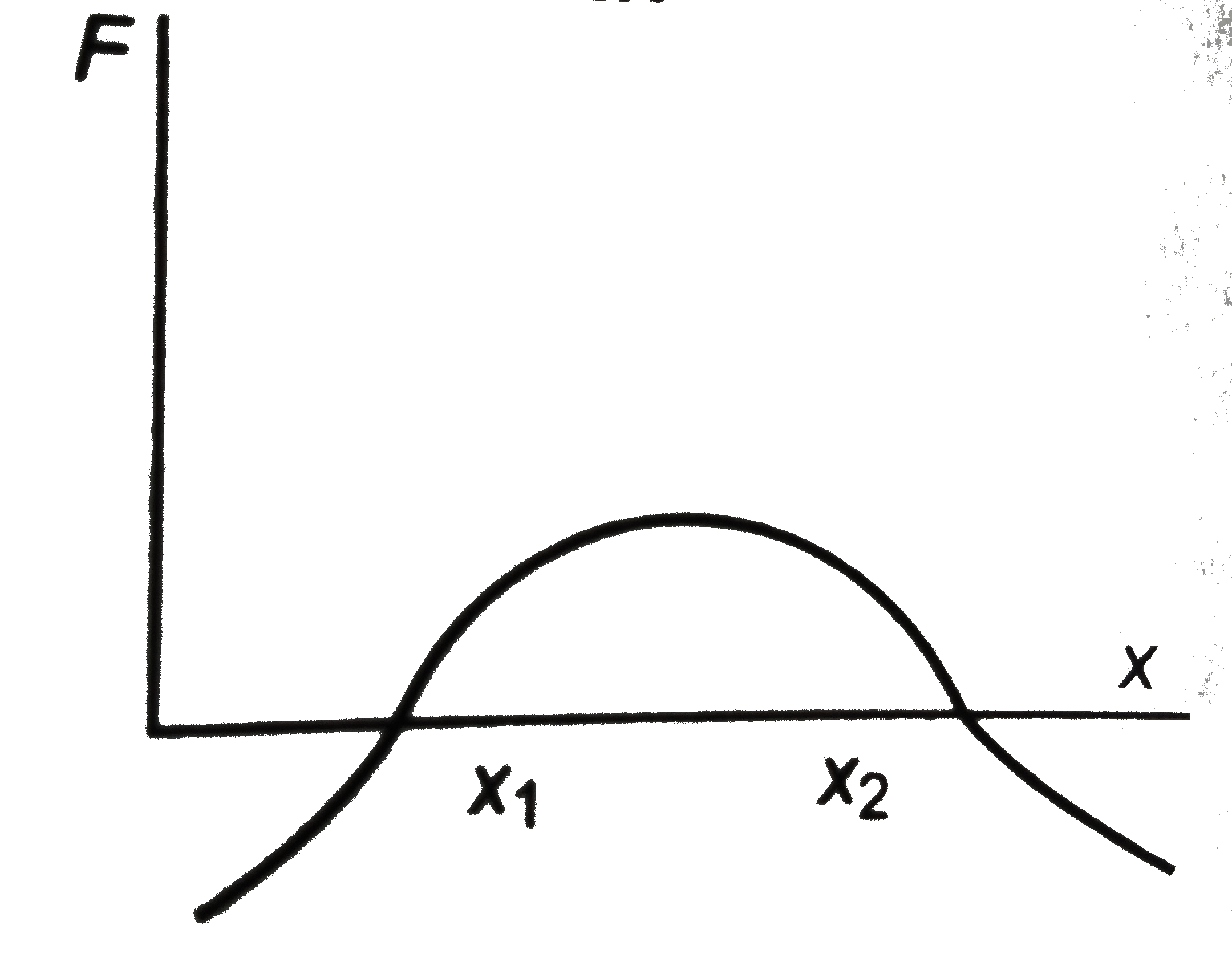 . View Solution
. View SolutionThe force acting on a body moving along x-axis variation of the particle particle shown in the figure. The body is in stable equilibrium at
 . View Solution
. View SolutionIf kinetic energy of a body is increasing then.
View SolutionThe variation of force F acting on a body moving along x - axis varies with its position (x) as shown in figure
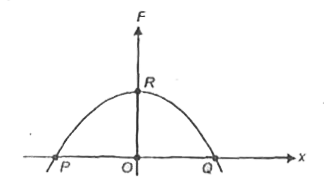
The body is in stable equilibrium stable atView SolutionThe kinetic energy of a body of mass 4 kg and momentum 6 N-s will be
View SolutionThe wavelength of a moving body of mass 0.1mg is 3.31×10−29m. The kinetic energy of the body in J would be :
View SolutionA body of mass 5 kg initially at rest is subjected to a force of 20 N. What is the kinetic energy acquired by the body at the end of 10 s?
View SolutionThe dependence of the acceleration of a body with time is shown in Figure. At t=0, the velocity of the body is −3m/s and position is x=0m.
 View Solution
View Solution

