An aeroplane is travelling at a height of 2000 m from the ground. The aeroplane, when at a point P, drops a bomb to hit a stationary target Q on the ground. In order that the bomb hits the target, what angle θ must the line PQ make with the vertical? [g=10ms−2]
![An aeroplane is travelling at a height of 2000 m from the ground. The aeroplane, when at a point P, drops a bomb to hit a stationary target Q on the ground. In order that the bomb hits the target, what angle theta must the line PQ make with the vertical? [g=10 ms^(-2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C02_S01_043_Q01.png)
45∘
30∘
60∘
90∘
The correct Answer is:A
Let t be the time taken by bomb to hit the target.
h=2000=12gt2⇒t=20s
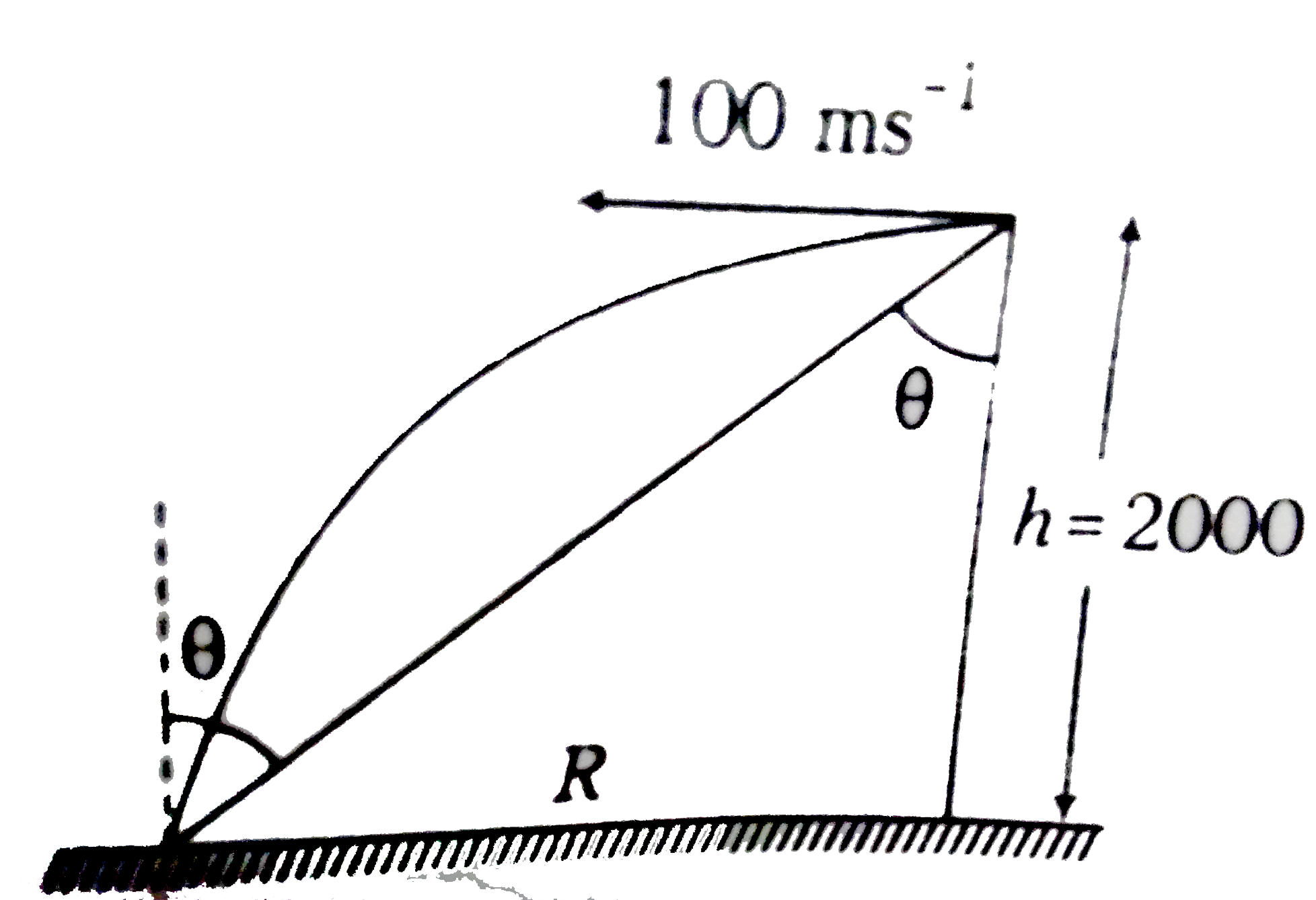
R=ut=(100)(20)=200m
∵tanθ=Rh=20002000=1⇒θ=45∘
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Taking it together
96 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Check Point 4.2
20 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
An aeroplane moving horizontally at a speed of 200m/s and at a height of 8.0×103m is to drop a bomb on a target. At what horizontal distance from the target should the bomb be released
View SolutionAn aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60∘ and 45∘ respectively. Find the vertical distance between the aeroplanes at that instant.
View Solution
Knowledge Check
An aeroplane flying horizontally with a speed of 360 km h−1 releases a bomb at a height of 490 m from the ground. If g = 9. 8 m s−2 , it will strike the ground at
A10 kmB100 kmC1 kmD16 km
An aeroplane flying horizontally at an altitude of 490m with a speed of 180 kmph drops a bomb. The horizontal distance at which it hits the ground is
View SolutionAn aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 600&450 respectively. Find the vertical distance between the aeroplanes at that instant.
View SolutionA ball is dropped from a height of 45m from the ground. The coefficient of restitution between the ball and the ground is 23. What is the distance travelled by the ball in 4th second of its motion. Assume negligible time is spent in rebounding. Let g=10ms2
View SolutionA helicopter while flying at a height of 100 m with velocity 30 m.s at an angle 30∘ with the horizontal, drops a packet. Where will the packet strike the ground ? ( g = 10 m/s2)
View SolutionA jet aeroplane is flying at a constant height of 2 km with a speed 360kmh−1 above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g=10ms−2)
View SolutionA bomb is dropped on an enemy post by an aeroplane flying with a horizontal velocity of 60km/hr and at a height of 490 m. How far the aeroplane must be from the enemy post at time of dropping the bomb, so that it may directly hit the target ?(g=9.8m/s2). What is the trajectory of the bomb as seen by an observer on the earth? What as seen by a person sitting inside the aeroplane?
View SolutionA rifle shoots a bullet with a muzzle velocity of 400ms−1 at a small target 400m away. The height above the target at which the bullet must be aimed to hit the target is (g=10ms−2).
View Solution
