A helicopter while flying at a height of 100 m with velocity 30 m.s at an angle 30∘ with the horizontal, drops a packet. Where will the packet strike the ground ? ( g = 10 m/s2)
To solve the problem of where the packet will strike the ground after being dropped from a helicopter flying at a height of 100 m with a velocity of 30 m/s at an angle of 30 degrees with the horizontal, we can follow these steps:
Step 1: Determine the components of the initial velocity
The initial velocity u of the packet can be broken down into horizontal and vertical components using trigonometric functions.
- Horizontal component ux=ucos(30∘)
- Vertical component uy=usin(30∘)
Given u=30m/s:
ux=30cos(30∘)=30×√32=15√3m/s
uy=30sin(30∘)=30×12=15m/s
Step 2: Use the kinematic equation to find the time of flight
We need to find the time t it takes for the packet to hit the ground. We can use the kinematic equation for vertical motion:
S=ut+12at2
Here, S=−100m (the packet falls 100 m), u=uy=15m/s, and a=−g=−10m/s2.
Substituting these values into the equation:
−100=15t−5t2
Rearranging gives us:
5t2−15t−100=0
Step 3: Solve the quadratic equation
We can simplify the equation by dividing by 5:
t2−3t−20=0
Now, we can apply the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−3,c=−20:
t=3±√(−3)2−4⋅1⋅(−20)2⋅1
Calculating the discriminant:
t=3±√9+802=3±√892
Calculating √89≈9.43:
t=3+9.432≈6.215s
Step 4: Calculate the horizontal distance (range)
Now that we have the time of flight, we can find the horizontal distance R where the packet will strike the ground:
R=ux⋅t
Substituting the values we found:
R=15√3⋅6.215
Calculating R:
R≈15⋅1.732⋅6.215≈15⋅10.75≈161.25m
Final Answer
The packet will strike the ground approximately 161.25 meters away from the point directly below where it was dropped.
---
The initial velocity u of the packet can be broken down into horizontal and vertical components using trigonometric functions.
- Vertical component uy=usin(30∘)
We need to find the time t it takes for the packet to hit the ground. We can use the kinematic equation for vertical motion:
We can simplify the equation by dividing by 5:
Now that we have the time of flight, we can find the horizontal distance R where the packet will strike the ground:
The packet will strike the ground approximately 161.25 meters away from the point directly below where it was dropped.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A bullet is projected upwards from the top of a tower of height 90 m with the velocity 30ms−1 making an angle 30∘ with the horizontal. Find the time taken by it to reach the ground is (g=10ms−2)
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
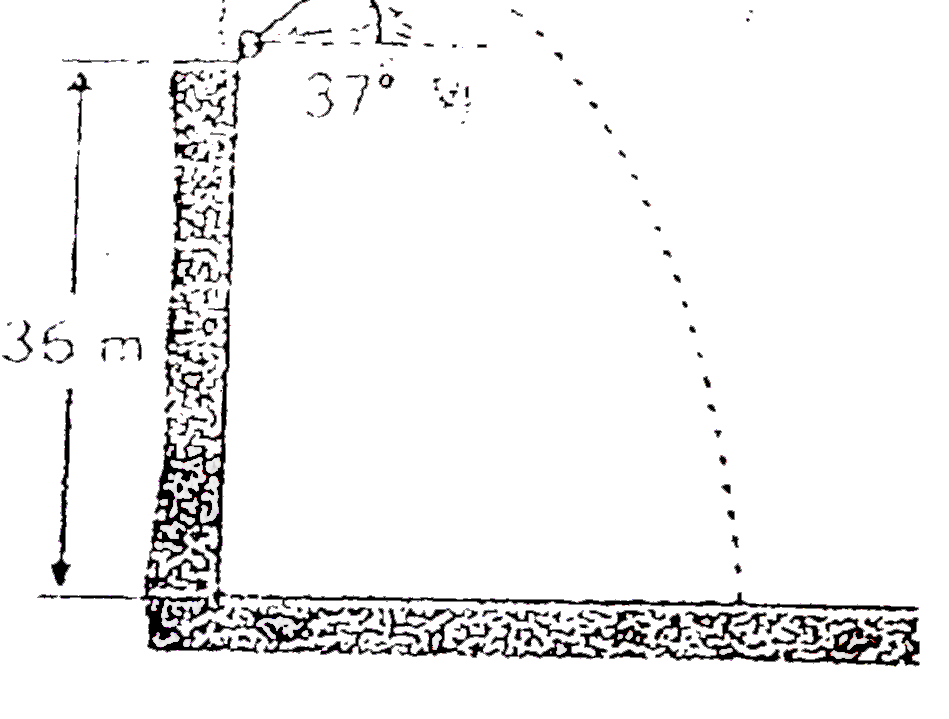 :
:
View SolutionA stone is projected from the ground with a velocity of 20 m/s at angle 30∘ with the horizontal. After one second it clears a wall then find height of the wall. (g=10ms−2)
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle 30∘ with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground?
(g=10m/s2)
View SolutionA boy playing on the roof of a 10m high building throws a ball with a speed of 10m/s at an angle of 30∘ with the horizontal. How far from the throwing point will the ball be at the height of 10m from the ground ?
[g=10m/s2,sin30∘=12,cos30∘=√32]
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionA stone is projected from the ground with velocity 50ms at an angle of 30∘. It crosses a wall after 3 sec. How far beyond the wall the stone will strike the ground (g=10msec2?
View Solution
