A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
tan−1(32)
tan−1(23)
tan−1(12)
tan−1(34)
The correct Answer is:B
To solve the problem of finding the angle of projection of a ball thrown to clear a wall, we can follow these steps:
Step 1: Understand the Problem
We have a ball thrown from the ground that needs to clear a wall that is 3 meters high and located 6 meters away from the throw point. The ball lands 18 meters beyond the wall, making the total horizontal distance from the throw point to where the ball lands 24 meters.
Step 2: Set Up the Variables
- Height of the wall (h) = 3 m
- Distance to the wall (d) = 6 m
- Total distance (R) = 24 m (6 m to the wall + 18 m beyond the wall)
- Acceleration due to gravity (g) = 9.81 m/s² (approximately)
Step 3: Use the Range Formula
The range R of a projectile is given by the formula:
R=u2sin2θg
Where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
From the problem, we have:
24=u2sin2θg
Rearranging gives:
u2g=24sin2θ
Let’s call this Equation (1).
Step 4: Use the Trajectory Equation
The height y of the projectile at a horizontal distance x is given by:
y=xtanθ−gx22u2cos2θ
Substituting y=3 m and x=6 m into the equation:
3=6tanθ−g⋅622u2cos2θ
This simplifies to:
3=6tanθ−36g2u2cos2θ
3=6tanθ−18gu2cos2θ
Now, substituting u2g from Equation (1):
3=6tanθ−1824sin2θcos2θ
This simplifies to:
3=6tanθ−18sin2θcos2θ24
3=6tanθ−3sin2θcos2θ4
Step 5: Solve for tanθ
Rearranging gives:
3+3sin2θcos2θ4=6tanθ
From the identity sin2θ=2sinθcosθ:
3+3⋅2sinθcos3θ4=6tanθ
This leads us to find tanθ in terms of sinθ and cosθ.
Step 6: Final Calculation
After simplifying, we find:
tanθ=69=23
Thus, the angle of projection θ is:
θ=tan−1(23)
Conclusion
The angle of projection of the ball is tan−1(23).
---
We have a ball thrown from the ground that needs to clear a wall that is 3 meters high and located 6 meters away from the throw point. The ball lands 18 meters beyond the wall, making the total horizontal distance from the throw point to where the ball lands 24 meters.
- Height of the wall (h) = 3 m
- Distance to the wall (d) = 6 m
- Total distance (R) = 24 m (6 m to the wall + 18 m beyond the wall)
- Acceleration due to gravity (g) = 9.81 m/s² (approximately)
The range R of a projectile is given by the formula:
R=u2sin2θg
Where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
24=u2sin2θg
Rearranging gives:
u2g=24sin2θ
Let’s call this Equation (1).
The height y of the projectile at a horizontal distance x is given by:
y=xtanθ−gx22u2cos2θ
Substituting y=3 m and x=6 m into the equation:
3=6tanθ−g⋅622u2cos2θ
This simplifies to:
3=6tanθ−36g2u2cos2θ
3=6tanθ−18gu2cos2θ
Now, substituting u2g from Equation (1):
3=6tanθ−1824sin2θcos2θ
This simplifies to:
3=6tanθ−18sin2θcos2θ24
3=6tanθ−3sin2θcos2θ4
Rearranging gives:
3+3sin2θcos2θ4=6tanθ
From the identity sin2θ=2sinθcosθ:
3+3⋅2sinθcos3θ4=6tanθ
This leads us to find tanθ in terms of sinθ and cosθ.
After simplifying, we find:
tanθ=69=23
Thus, the angle of projection θ is:
θ=tan−1(23)
The angle of projection of the ball is tan−1(23).
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance12videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective19videos
MEASUREMENT AND ERRORS
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
Similar Questions
A ball is thrown from ground level so as to just clear a wall 4 m high at a distance of 4 m and fall at a distance of 14 m from the wall. Find the magnitude and direction of the velocity of the ball.
View SolutionA ball is thrown from the ground so that it just crosses a wall 5m high at a distance of 10m and falls at a distance of 10m ahead from the wall. Find the speed and the direction of projection of ball. Assume, g=10 ms–2
View SolutionA ball is projected from ground in such a way that after 10 seconds of projection it lands on ground 500 m away from the point of projection. Find out :-
(i) angle of projection
(ii) velocity of projection
(iii) Velocity of ball after 5 secondsView SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA shell fired from the ground is just able to cross horizontally the top of a wall 90m away and 45m high. The direction of projection of the shell will be.
View SolutionA ball is thrown horizontally from the top of a lower of unkown height .Ball strikes a vertical wall whose plane is normal to the plane of month of ball Collison is elastic and ball falls on ground exactly at the midpoints between the lower and the wall ball strikes the grouind at an angle of the 30∘ with horizontal .Find the hieght of the tower (in meter)
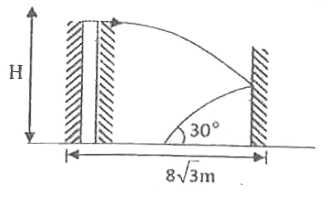 View Solution
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
 View Solution
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View Solution

