A cricket ball thrown across a field is a heights h1 and h2 from the point of projection at time t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
(h1t22−h2t21h1t2−h2t1)
(h1t22−h2t21h1t2−h2t1)
(h1t22−h2t21h1t2−h2t1)
None of these
The correct Answer is:C
To find the time of flight of a cricket ball thrown across a field and caught at the same height from which it was thrown, we can use the principles of projectile motion. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a cricket ball thrown at an angle with an initial velocity u. It reaches heights h1 and h2 at times t1 and t2 respectively. The ball is caught at the same height from which it was thrown.
Step 2: Write the Equations for Vertical Motion
The vertical motion of the ball can be described using the following kinematic equation:
h=uyt−12gt2
where uy=usinθ is the vertical component of the initial velocity, g is the acceleration due to gravity, and t is the time.
For the heights h1 and h2:
1. At time t1:
h1=usinθ⋅t1−12gt21
2. At time t2:
h2=usinθ⋅t2−12gt22
Step 3: Rearranging the Equations
We can rearrange both equations to isolate usinθ:
1. From the first equation:
usinθ=h1+12gt21t1
2. From the second equation:
usinθ=h2+12gt22t2
Step 4: Set the Two Expressions Equal
Since both expressions equal usinθ, we can set them equal to each other:
h1+12gt21t1=h2+12gt22t2
Step 5: Cross-Multiply and Simplify
Cross-multiplying gives:
(h1+12gt21)t2=(h2+12gt22)t1
Expanding both sides leads to:
h1t2+12gt21t2=h2t1+12gt22t1
Step 6: Rearranging for Time of Flight
We know that the total time of flight T for a projectile is given by:
T=2usinθg
Using the expressions for usinθ derived earlier, we can substitute back to find T.
Step 7: Final Expression for Time of Flight
After performing the necessary algebraic manipulations, we arrive at the final expression for the total time of flight:
T=h1t22−h2t21h1t2−h2t1
Conclusion
Thus, the time of flight of the ball is:
T=h1t22−h2t21h1t2−h2t1
We have a cricket ball thrown at an angle with an initial velocity u. It reaches heights h1 and h2 at times t1 and t2 respectively. The ball is caught at the same height from which it was thrown.
The vertical motion of the ball can be described using the following kinematic equation:
h=uyt−12gt2
where uy=usinθ is the vertical component of the initial velocity, g is the acceleration due to gravity, and t is the time.
1. At time t1:
h1=usinθ⋅t1−12gt21
2. At time t2:
h2=usinθ⋅t2−12gt22
We can rearrange both equations to isolate usinθ:
1. From the first equation:
usinθ=h1+12gt21t1
2. From the second equation:
usinθ=h2+12gt22t2
Since both expressions equal usinθ, we can set them equal to each other:
h1+12gt21t1=h2+12gt22t2
Cross-multiplying gives:
(h1+12gt21)t2=(h2+12gt22)t1
Expanding both sides leads to:
h1t2+12gt21t2=h2t1+12gt22t1
We know that the total time of flight T for a projectile is given by:
T=2usinθg
Using the expressions for usinθ derived earlier, we can substitute back to find T.
After performing the necessary algebraic manipulations, we arrive at the final expression for the total time of flight:
T=h1t22−h2t21h1t2−h2t1
Thus, the time of flight of the ball is:
T=h1t22−h2t21h1t2−h2t1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - C. Medical entrances gallery1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective19videos
MEASUREMENT AND ERRORS
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
Similar Questions
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
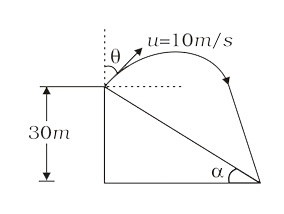
The time of flight of the ball is:View Solution
Knowledge Check
- Question 1 - Select One
A cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
A2 sB3 sC4 sD5 s
A ball is projected vertically up such that it passes thorugh a fixed point after a time t1 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .View Solution
.View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is thrown vertically upwards. It was observed at a height h twice after a time interval Δt. The initial velocity of the ball is
View SolutionA body throws a ball from shoulder height at an initial velocity of 30 m/s. Spending 4.8 s in air, the ball is caught by another boy as the same shoulder-height level. What is the angle of projection ?
View SolutionTwo balls are dropped from heights h and 2h respectively from the earth surface. The ratio of time of these balls to reach the earth is.
View SolutionA ball is thrown from the top of a tower in vertically upward direction. Velocity at a point h m below the point of projection is twice of the velocity at a point h m above the point of projection. Find the maximum height reached by the ball above the top of tower.
View Solution

