IN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
To solve the problem, we need to analyze the forces acting on the person who is resting against the inner wall of the rotating cylindrical rotor. The key forces to consider are the gravitational force acting downward and the frictional force acting upward.
1. Identify the Forces:
- The gravitational force acting on the person is Fg=mg, where m is the mass of the person and g is the acceleration due to gravity.
- The normal force N exerted by the wall on the person provides the centripetal force necessary for circular motion. This force is given by N=mv2r, where v is the tangential speed and r is the radius of the rotor.
2. Frictional Force:
- The static frictional force Fs that prevents the person from slipping down is given by Fs=μN, where μ is the coefficient of static friction.
3. Set Up the Equation:
- At the point where the floor is removed, the person will not slip if the frictional force is equal to the gravitational force. Thus, we can write the equation:
Fs=Fg
Substituting the expressions for these forces, we get:
μN=mg
4. Substituting for Normal Force:
- Substitute N=mv2r into the equation:
μ(mv2r)=mg
5. Canceling Mass:
- Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
μv2r=g
6. Rearranging for Speed:
- Rearranging the equation to solve for v2:
v2=rgμ
7. Taking the Square Root:
- Taking the square root to find v:
v=√rgμ
8. Substituting Values:
- Now, substitute the given values:
- r=2m
- g=10m/s2
- μ=0.2
v=√2×100.2=√200.2=√100=10m/s
Final Answer:
The minimum speed at which the floor may be removed is 10m/s.
- The gravitational force acting on the person is Fg=mg, where m is the mass of the person and g is the acceleration due to gravity.
- The normal force N exerted by the wall on the person provides the centripetal force necessary for circular motion. This force is given by N=mv2r, where v is the tangential speed and r is the radius of the rotor.
- The static frictional force Fs that prevents the person from slipping down is given by Fs=μN, where μ is the coefficient of static friction.
- At the point where the floor is removed, the person will not slip if the frictional force is equal to the gravitational force. Thus, we can write the equation:
Fs=Fg
Substituting the expressions for these forces, we get:
μN=mg
- Substitute N=mv2r into the equation:
μ(mv2r)=mg
- Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
μv2r=g
- Rearranging the equation to solve for v2:
v2=rgμ
- Taking the square root to find v:
v=√rgμ
- Now, substitute the given values:
- r=2m
- g=10m/s2
- μ=0.2
v=√2×100.2=√200.2=√100=10m/s
The minimum speed at which the floor may be removed is 10m/s.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples5videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
In a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15 m What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View Solution
Knowledge Check
- Question 1 - Select One
A 4m long ladder weighing 25kg rests with its upper end against a smooth wall and lower end on rough ground.What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
Aa. 0.19Bb. 0.29Cc. 0.39Dd. 0.49
A block of weight 30 N is in contact with a rough wall. A force of 50 N is applied as shown in the figure. Find the coefficient of static friction between the wall and the block assuming the block is just about to slip.
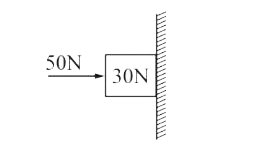 View Solution
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
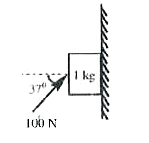 View Solution
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA person wants to drive on the vertical suirface of a large cylindrical wooden well commonly known as deathwell in a circus. The radius of the well 2 meter, and the coefficient of friction between the tyers of the motorcycle and the wall of the well is 0.2 the minimum speed the motorcyclist must have in order to prevent slipping should be
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is (g=10m/s2)
 View Solution
View Solution

