A block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is . Find the magnitude of the force exerted by the wall on the block :
12 N
5 N
7.2 N
13 N
The correct Answer is:D
To solve the problem, we need to find the total force exerted by the wall on the block. Let's break it down step by step.
Step 1: Identify the Forces Acting on the Block
- The weight of the block (W) acting downwards = 5 N.
- The applied force (F) pushing the block against the wall = 12 N.
- The normal force (N) exerted by the wall on the block, which acts horizontally and is equal in magnitude to the applied force = 12 N.
- The frictional force (f) acting upwards, which opposes the weight of the block.
Step 2: Calculate the Maximum Frictional Force
The maximum frictional force can be calculated using the formula:
fmax=μ⋅N
Where:
- μ = coefficient of friction = 0.6
- N = normal force = 12 N
Substituting the values:
fmax=0.6⋅12=7.2N
Step 3: Compare the Weight and Frictional Force
The weight of the block is 5 N, and the maximum frictional force is 7.2 N. Since the maximum frictional force is greater than the weight of the block, the frictional force will be equal to the weight of the block in this case to maintain equilibrium.
Thus, the frictional force (f) acting upwards is:
f=W=5N
Step 4: Calculate the Total Force Exerted by the Wall
The total force exerted by the wall on the block consists of two components:
1. The normal force (N) = 12 N (horizontal)
2. The frictional force (f) = 5 N (vertical)
To find the resultant force (F_net) exerted by the wall on the block, we can use the Pythagorean theorem:
Fnet=√N2+f2
Substituting the values:
Fnet=√(12)2+(5)2
Fnet=√144+25
Fnet=√169
Fnet=13N
Final Answer
The magnitude of the force exerted by the wall on the block is 13 N.
---
- The weight of the block (W) acting downwards = 5 N.
- The applied force (F) pushing the block against the wall = 12 N.
- The normal force (N) exerted by the wall on the block, which acts horizontally and is equal in magnitude to the applied force = 12 N.
- The frictional force (f) acting upwards, which opposes the weight of the block.
The maximum frictional force can be calculated using the formula:
fmax=μ⋅N
Where:
- μ = coefficient of friction = 0.6
- N = normal force = 12 N
fmax=0.6⋅12=7.2N
The weight of the block is 5 N, and the maximum frictional force is 7.2 N. Since the maximum frictional force is greater than the weight of the block, the frictional force will be equal to the weight of the block in this case to maintain equilibrium.
f=W=5N
The total force exerted by the wall on the block consists of two components:
1. The normal force (N) = 12 N (horizontal)
2. The frictional force (f) = 5 N (vertical)
Fnet=√N2+f2
Fnet=√(12)2+(5)2
Fnet=√144+25
Fnet=√169
Fnet=13N
The magnitude of the force exerted by the wall on the block is 13 N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Chapter exercises (A) Taking it together
71 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
These questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following four responses
Assertion A block of weight 10 N is pushed against a vertical wall by a force of 15 N. The coefficient of friction between the wall and the block is 0.6. Then, the magnitude of maximum frictional force is 9 N.
Reason For given system block will remain stationary.
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
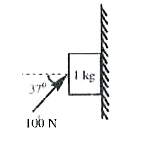
View Solution
Knowledge Check
A 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
A0.5m/s2B1m/s2C5m/s2D7.5m/s2
A block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionGiven in the figure are two blocks A and B of weight 20 N and 100 N respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is
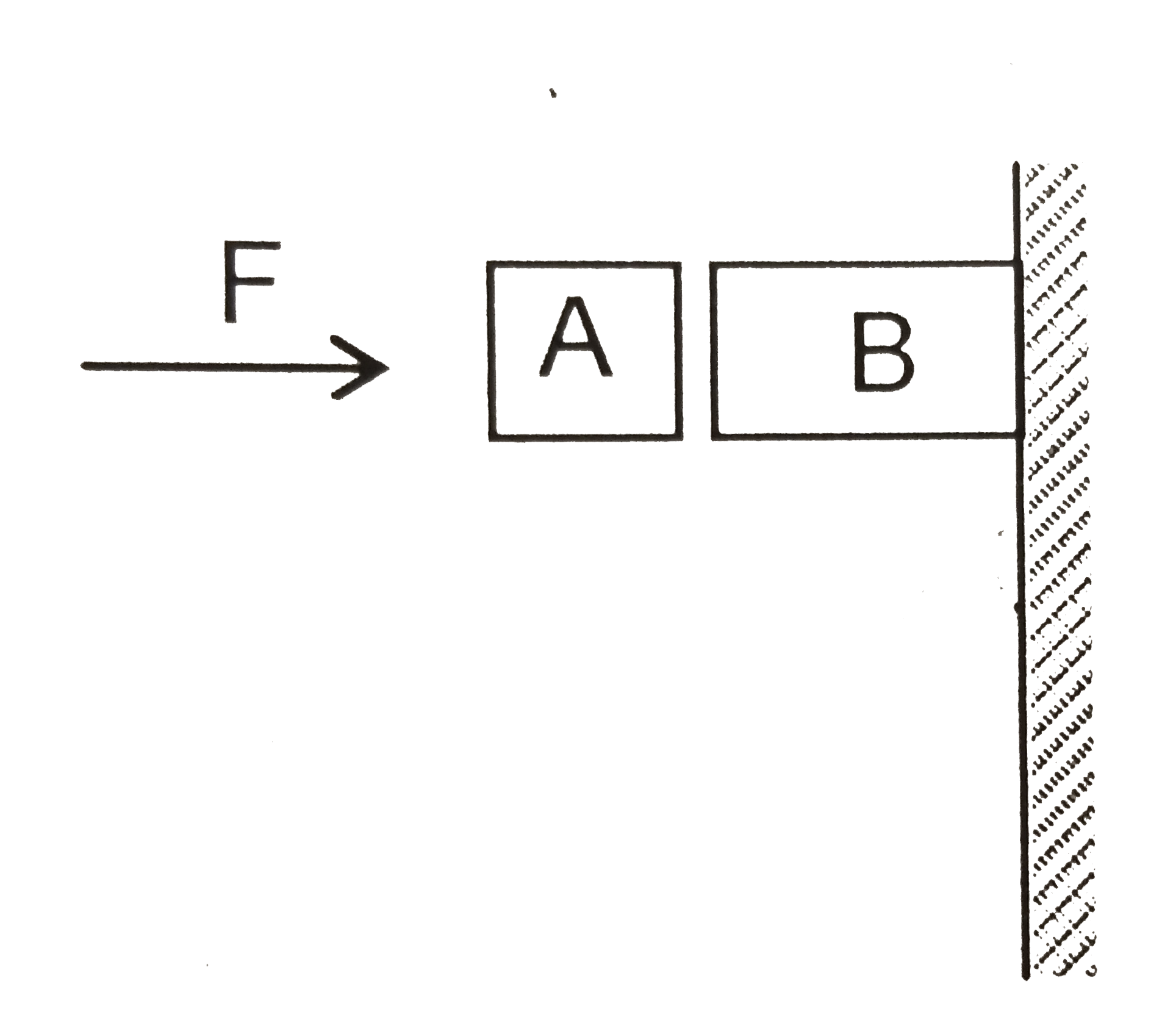
View SolutionA block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View Solution
