Question

A hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is ${\displaystyle \theta }$, find the angular speed at which the bowl is rotating.

Explanation

Let `omega` be the angular speed of rotation of the bowl. Two forces are acting on the ball.
(i) normal reaction N
(ii) weight mg

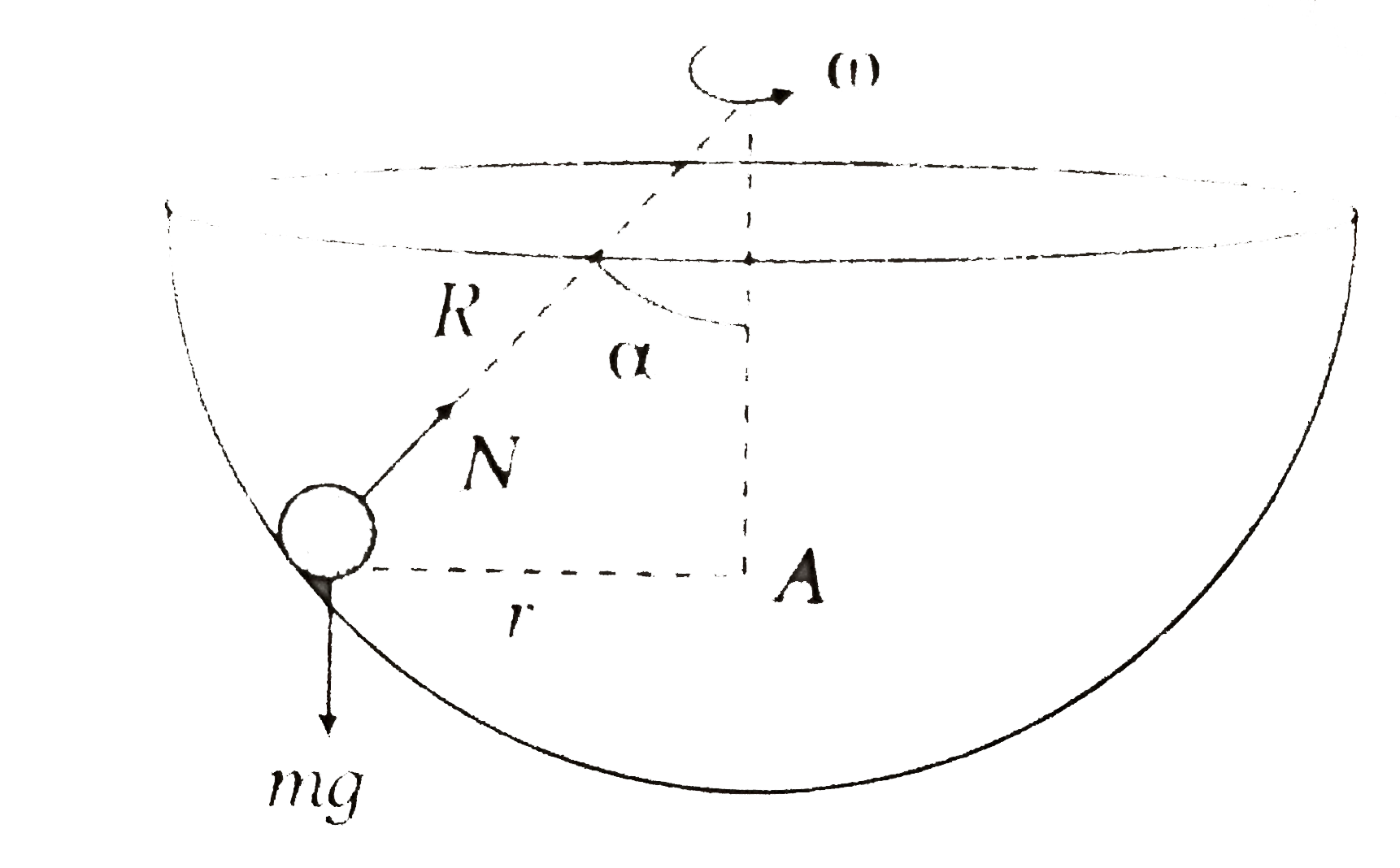
The ball is rotating in a circle of radius `r=(Rsinalpha)` with centre at A at an angular speed `omega`. Thus,
`Nsinalpha=mromega^(2)=mRomega^(2)sintheta`.....(i)
and `Ncosalpha=mg`....(ii)
Dividing Eqs. (i) by (ii), we get
`(1)/(cosalpha)=(omega^(2)R)/(g)rArromega=sqrt((g)/(Rcosalpha))`