Gravitational force between a point mass m and M separated by a distance is F. Now if a point mass 2m is placed next to m is contact with it. The force on M due to m and the total force on M are
2F, F
F, 2F
F, 3F
F, F
The correct Answer is:C
To solve the problem, we will analyze the gravitational forces acting on mass M due to the masses m and 2m.
1. Understanding the Initial Force:
The gravitational force F between the point mass M and mass m is given by the formula:
F=G⋅M⋅mr2
where G is the gravitational constant and r is the distance between the two masses.
2. Introducing the Second Mass:
Now, we place a second mass 2m next to mass m. The distance between mass M and mass m remains the same, while the distance between mass M and mass 2m is also the same.
3. Calculating the Force on M Due to 2m:
The gravitational force F′ between mass M and mass 2m can be calculated as:
F′=G⋅M⋅2mr2
This can be simplified as:
F′=2⋅G⋅M⋅mr2=2F
4. Calculating the Total Force on M:
The total gravitational force Ftotal on mass M due to both masses m and 2m is the sum of the individual forces:
Ftotal=F+F′=F+2F=3F
5. Conclusion:
Therefore, the force on M due to mass m is F, and the total force on M due to both masses m and 2m is 3F.
Final Answer:
- The force on M due to m is F.
- The total force on M is 3F.
The gravitational force F between the point mass M and mass m is given by the formula:
F=G⋅M⋅mr2
where G is the gravitational constant and r is the distance between the two masses.
Now, we place a second mass 2m next to mass m. The distance between mass M and mass m remains the same, while the distance between mass M and mass 2m is also the same.
The gravitational force F′ between mass M and mass 2m can be calculated as:
F′=G⋅M⋅2mr2
This can be simplified as:
F′=2⋅G⋅M⋅mr2=2F
The total gravitational force Ftotal on mass M due to both masses m and 2m is the sum of the individual forces:
Ftotal=F+F′=F+2F=3F
Therefore, the force on M due to mass m is F, and the total force on M due to both masses m and 2m is 3F.
- The force on M due to m is F.
- The total force on M is 3F.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.3
15 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Gravitational force between two point masses m and M separated by a distance r is F. Now if a point mass 3m is placed next to m, what will be the (a) force on M due to m, (b) total force on M?
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View Solution
Knowledge Check
Two point masses A and B having masses in the ratio 4:3 are separated by a distance of 1m. When another point mass C of mass M is placed in between A and B, the force between A and C is (13)rd of the force between B and C. Then the distance C from A is
A23mB13mC14mD27mTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2The gravitational force F between two masses m1andm2 separeted by a distance r is given by
F=Gm1m2r2
Where G is the universal gravitational constant. What are the dimensions of G ?AM−1L2T−3BM−1L3T−2CML3T−2DML2T−3
Two bodies of mass M and 4M kept at a distance y apart. Where should a small particle of mass m be placed from M so that the net gravitational force on it is zero
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View SolutionA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
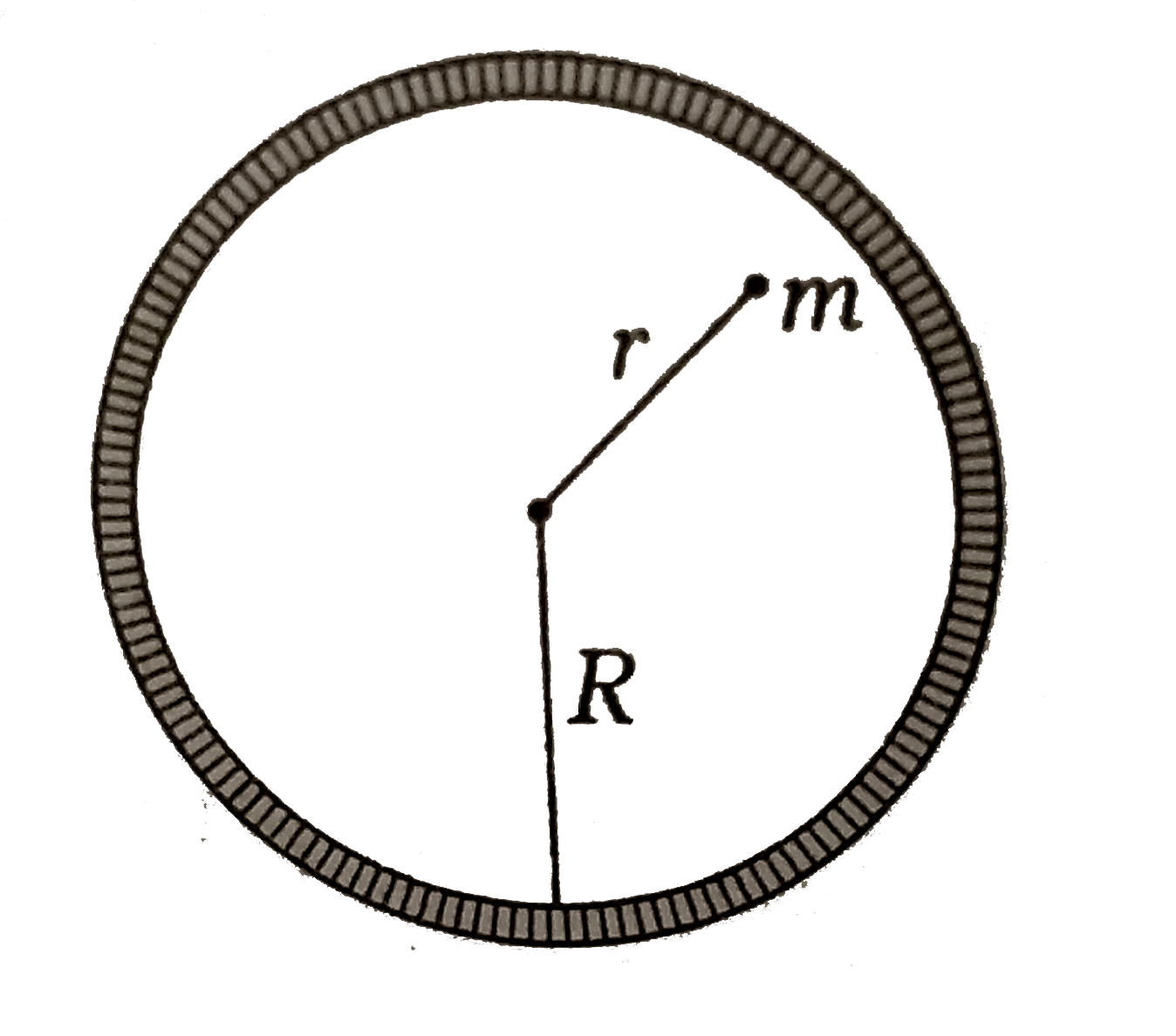
View SolutionWrite an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r .
View SolutionThe gravitational force on a body of mass 1.5 kg situated at a point is 45 M . The gravitational field intensity at that point is .
View Solution