Three equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
2
√2
1
zero
The correct Answer is:D
To find the force acting on the mass of 4 kg placed at the centroid of the equilateral triangle formed by three 2 kg masses, we can follow these steps:
Step 1: Understand the Configuration
We have three equal masses (2 kg each) located at the vertices of an equilateral triangle. A mass of 4 kg is placed at the centroid of the triangle. The distance from the centroid to each vertex is given as √2 m.
Step 2: Calculate the Gravitational Force Between Each Vertex Mass and the Centroid Mass
The gravitational force F between two masses can be calculated using Newton's law of gravitation:
F=G⋅m1⋅m2r2
where:
- G is the gravitational constant (6.674×10−11N m2/kg2)
- m1 and m2 are the masses (2 kg and 4 kg)
- r is the distance between the masses (√2m)
Substituting the values:
F=(6.674×10−11)⋅(2)⋅(4)(√2)2
F=(6.674×10−11)⋅82
F=53.392×10−112
F=26.696×10−11N
Step 3: Analyze the Forces Acting on the 4 kg Mass
Each of the three 2 kg masses exerts a gravitational force on the 4 kg mass. Since the triangle is equilateral, the angles between the forces are 120 degrees.
Step 4: Calculate the Resultant Force
To find the net force acting on the 4 kg mass, we can use vector addition. The forces from two of the masses will have components that can be resolved into horizontal and vertical directions.
1. The force from one mass can be represented as:
- F1=26.696×10−11N at an angle of 0∘
- F2=26.696×10−11N at an angle of 120∘
- F3=26.696×10−11N at an angle of 240∘
2. The horizontal components of F2 and F3 will cancel out due to symmetry, and the vertical components will also cancel out.
Step 5: Conclusion
Since the forces from the three masses are symmetrically arranged and cancel each other out, the net gravitational force acting on the mass of 4 kg at the centroid is:
Fnet=0N
Final Answer
The force acting on the mass of 4 kg is 0N.
---
We have three equal masses (2 kg each) located at the vertices of an equilateral triangle. A mass of 4 kg is placed at the centroid of the triangle. The distance from the centroid to each vertex is given as √2 m.
The gravitational force F between two masses can be calculated using Newton's law of gravitation:
F=G⋅m1⋅m2r2
where:
- G is the gravitational constant (6.674×10−11N m2/kg2)
- m1 and m2 are the masses (2 kg and 4 kg)
- r is the distance between the masses (√2m)
F=(6.674×10−11)⋅(2)⋅(4)(√2)2
F=(6.674×10−11)⋅82
F=53.392×10−112
F=26.696×10−11N
Each of the three 2 kg masses exerts a gravitational force on the 4 kg mass. Since the triangle is equilateral, the angles between the forces are 120 degrees.
To find the net force acting on the 4 kg mass, we can use vector addition. The forces from two of the masses will have components that can be resolved into horizontal and vertical directions.
- F1=26.696×10−11N at an angle of 0∘
- F2=26.696×10−11N at an angle of 120∘
- F3=26.696×10−11N at an angle of 240∘
Since the forces from the three masses are symmetrically arranged and cancel each other out, the net gravitational force acting on the mass of 4 kg at the centroid is:
Fnet=0N
The force acting on the mass of 4 kg is 0N.
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Check Point 10.2
Explore 20 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Check Point 10.3
Explore 15 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Level 2 Subjective
Explore 14 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Three equal masses of 1 kg each are placed at the vertices of an equilateral ΔPQR and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of √2m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle and other particle of mass 2kg is placed on centroid of triangle which is at a distance of √2 m from each of the vertices of the triangle .The force in newton , acting on the particle of mass 2 kg is
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
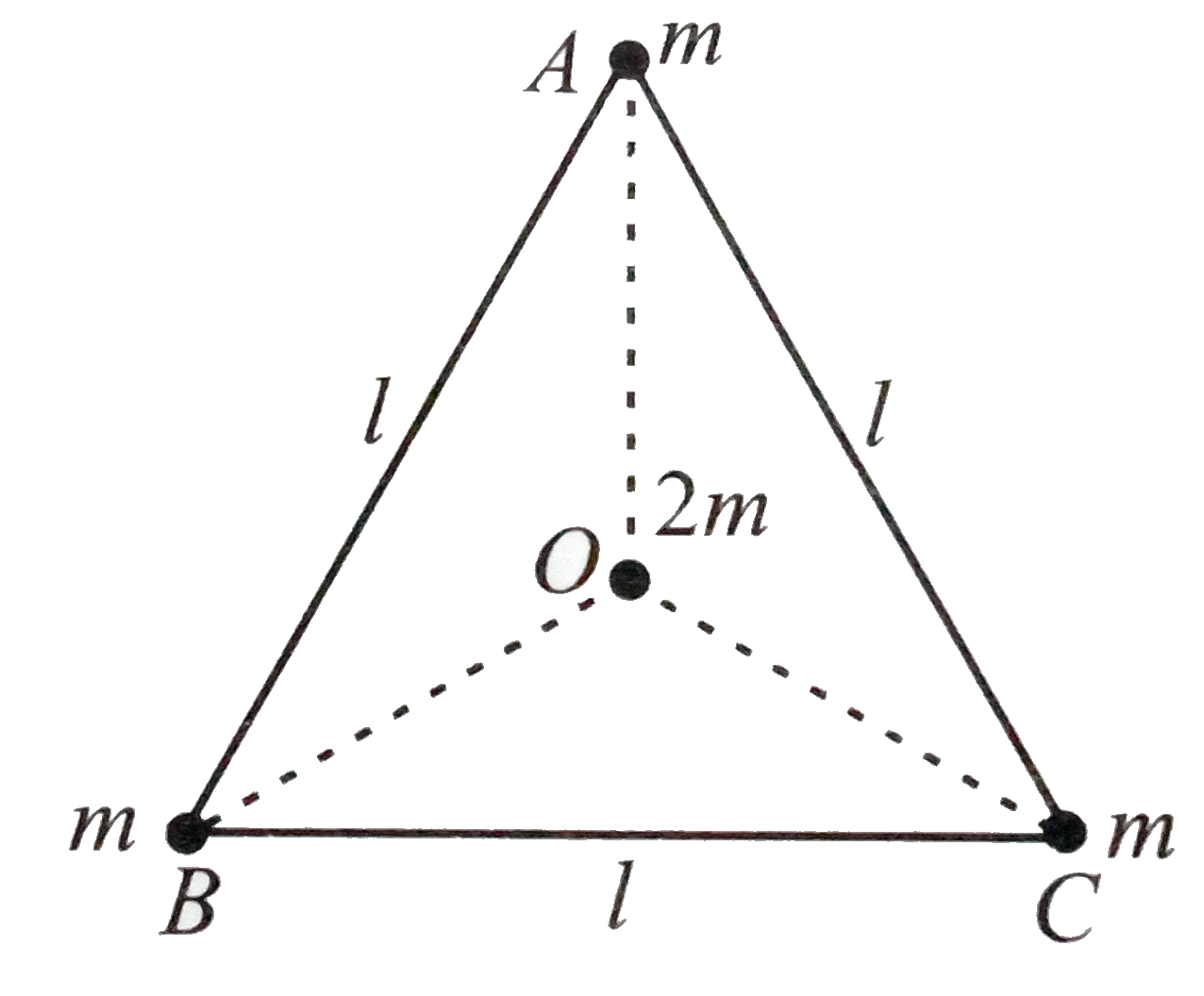 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Three equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
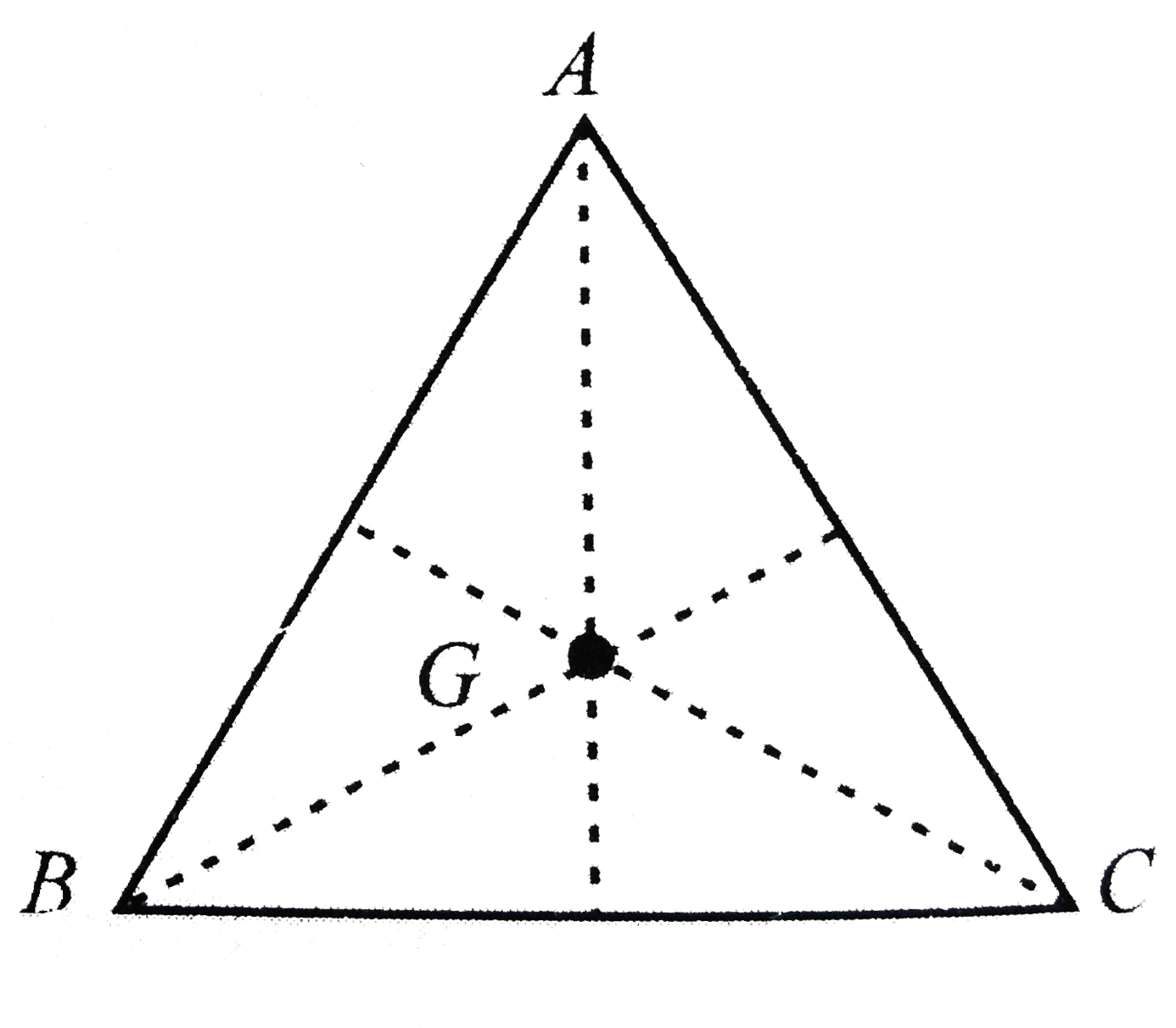
View SolutionThree equal masses of mkg each are fixed at the vertices of an equilateral triangle ABC.
a. What is the force acting on a mass 2m placed at the centroid G of the triangle?
b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
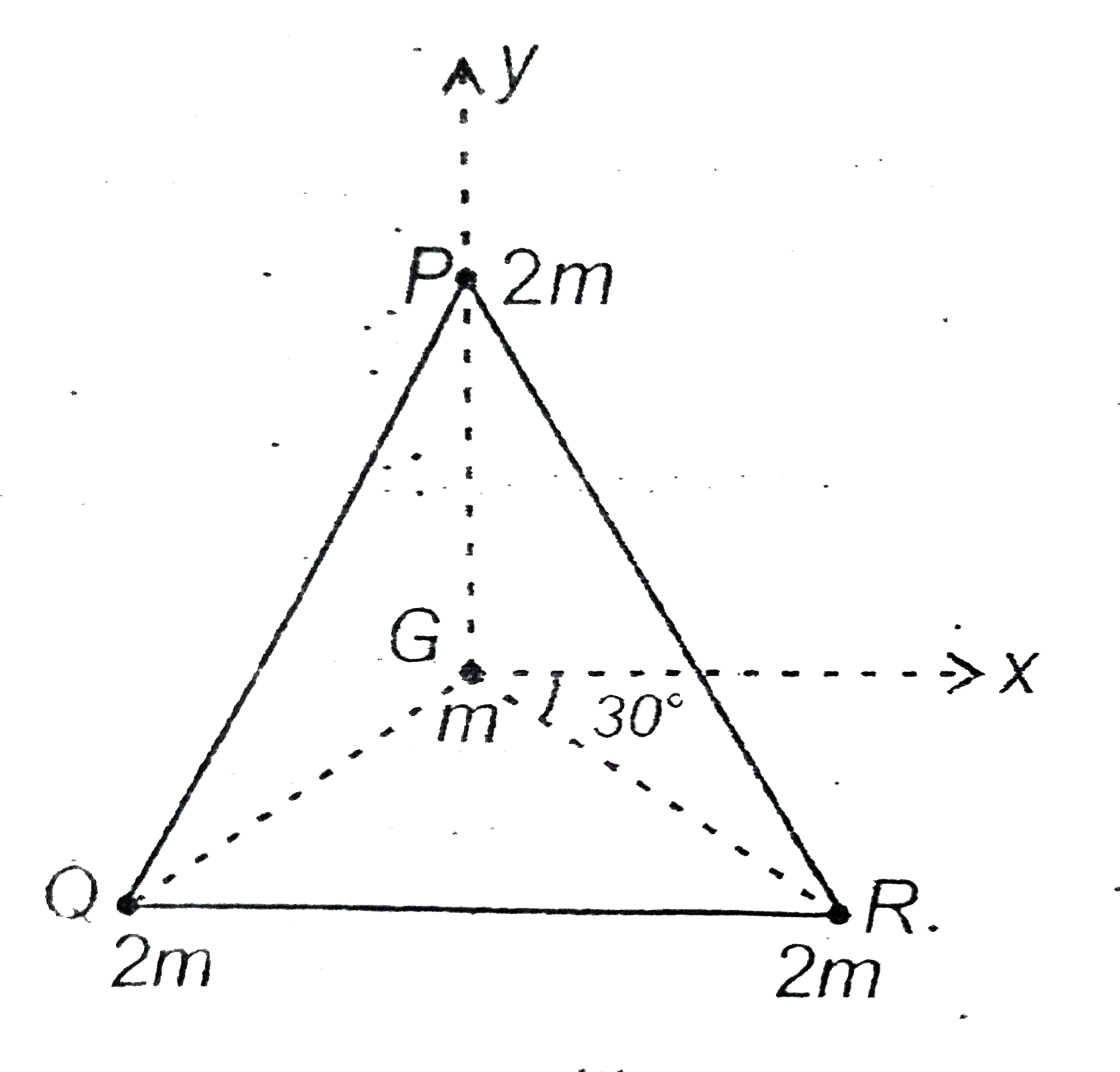
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View Solution
