Two bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
V=−Gd(m+M)
V=−Gmd
V=−GMd
V=−Gd(√m+√M)2
The correct Answer is:D
Enet=0
∴Gmx2=GM(d−x)2,x is distance from m
∴xd−x=√m√M⇒x=√m√m+√M,d
and d−x=√M√m+√M.d
Since, gravitational potential between two bodies of masses M and m respectively, is given by
V=−Gmx−GMd−x
=−GM(√m+√M)√m.d−GM√m+√M√M.d=−Gd(√m+√M)2.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.4
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero,the gravitational potential will be :-
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)
Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point due to mass m on the line joining where gravitational field is zero
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo point masses having mass m and 2m are placed at distance d . The point on the line joining point masses , where gravitational field intensity is zero will be at distance
View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionTwo bodies of mass 102 kg and 103 kg are lying 1 m apart .
The gravitational potential at the mid-point of the line joining them is
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionTwo spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
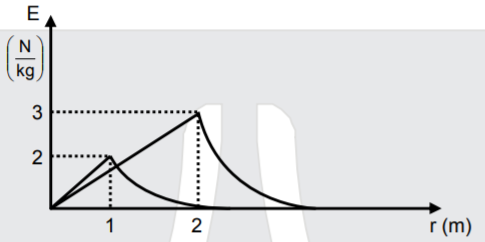 -
-
View Solution
