For a uniform ring of mass M and radius R at its centre
field and potential both are zero
field is zero but potential is GMR
field is zero but potential is −GM/R
magnitude of field is GMR2 and potential −GMR
The correct Answer is:C
To solve the question regarding the gravitational field and potential at the center of a uniform ring of mass M and radius R, we will analyze the gravitational field and gravitational potential step by step.
Step 1: Understanding Gravitational Field
The gravitational field →E at a point is defined as the force experienced by a unit mass placed at that point. For a uniform ring, we need to consider the symmetry of the ring.
Step 2: Gravitational Field at the Center
At the center of the ring, due to symmetry, the gravitational forces exerted by the mass elements of the ring cancel each other out. Therefore, the net gravitational field →E at the center of the ring is:
→E=0
Step 3: Understanding Gravitational Potential
The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point against the gravitational field.
Step 4: Gravitational Potential at the Center
The gravitational potential V due to a mass M at a distance r is given by the formula:
V=−GMr
For a point at the center of the ring, the distance from any mass element of the ring to the center is equal to the radius R of the ring. Therefore, the gravitational potential at the center of the ring is:
V=−GMR
Conclusion
Thus, at the center of a uniform ring of mass M and radius R:
- The gravitational field E is 0.
- The gravitational potential V is −GMR.
Final Answer
- Gravitational Field E=0
- Gravitational Potential V=−GMR
---
The gravitational field →E at a point is defined as the force experienced by a unit mass placed at that point. For a uniform ring, we need to consider the symmetry of the ring.
At the center of the ring, due to symmetry, the gravitational forces exerted by the mass elements of the ring cancel each other out. Therefore, the net gravitational field →E at the center of the ring is:
The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point against the gravitational field.
The gravitational potential V due to a mass M at a distance r is given by the formula:
Thus, at the center of a uniform ring of mass M and radius R:
- The gravitational field E is 0.
- The gravitational potential V is −GMR.
- Gravitational Field E=0
- Gravitational Potential V=−GMR
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.410videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.520videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.220videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2

A uniform dics of mass m and radius R=8023π2m is pivoted smoothly at P. If a uniform ring of mass m and radius R is welded at the lowest point of the disc, find the period of SHM of the system (disc + ring). (in seconds)View SolutionFind the moment of inertia, about a diameter, of a uniform ring of mass M = 8kg and radius a = 1m?
 View Solution
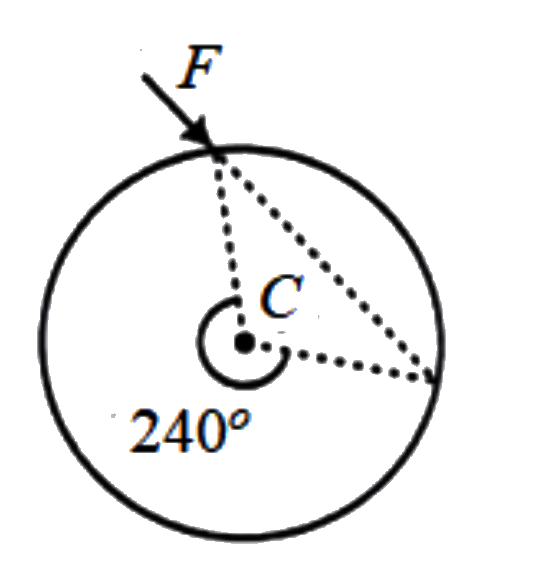
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
 View Solution
View SolutionTwo equal and opposite forces F are allplied tangentially to a uniform disc of mass M and radius R . If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,View Solution
,View Solution

