A planet of mass m is in an elliptical orbit about the sun (m << Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
2mAT
mAT
mA2T
2mAT
The correct Answer is:A
Considering Kepler's second law we know that
AT=L2morL=2mAT.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A planet of mass m is in an elliptical orbit about the sun (m << Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View SolutionA planet of mass m is the elliptical orbit about the sun (m<<Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View Solution
Knowledge Check
A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View Solution
A planet of mass m moves in an elliptical orbit around sun with sun at its Focus. (e=eccentricity of ellipse). Then TACB/TBDA is [TACB is time taken to travel from A to C B & TBDA is time taken to travel from B to D to A]
View SolutionA satellite of mass m is in an elliptical orbit around the earth of mass M(M>>m) the speed of the satellite at its nearest point ot the earth (perigee) is √6GM5R where R= its closest distance to the earth it is desired to transfer this satellite into a circular orbit around the earth of radius equal its largest distance from the earth. Find the increase in its speed to be imparted at the apogee (farthest point on the elliptical orbit).
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
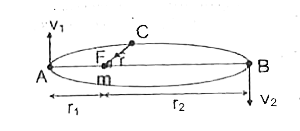
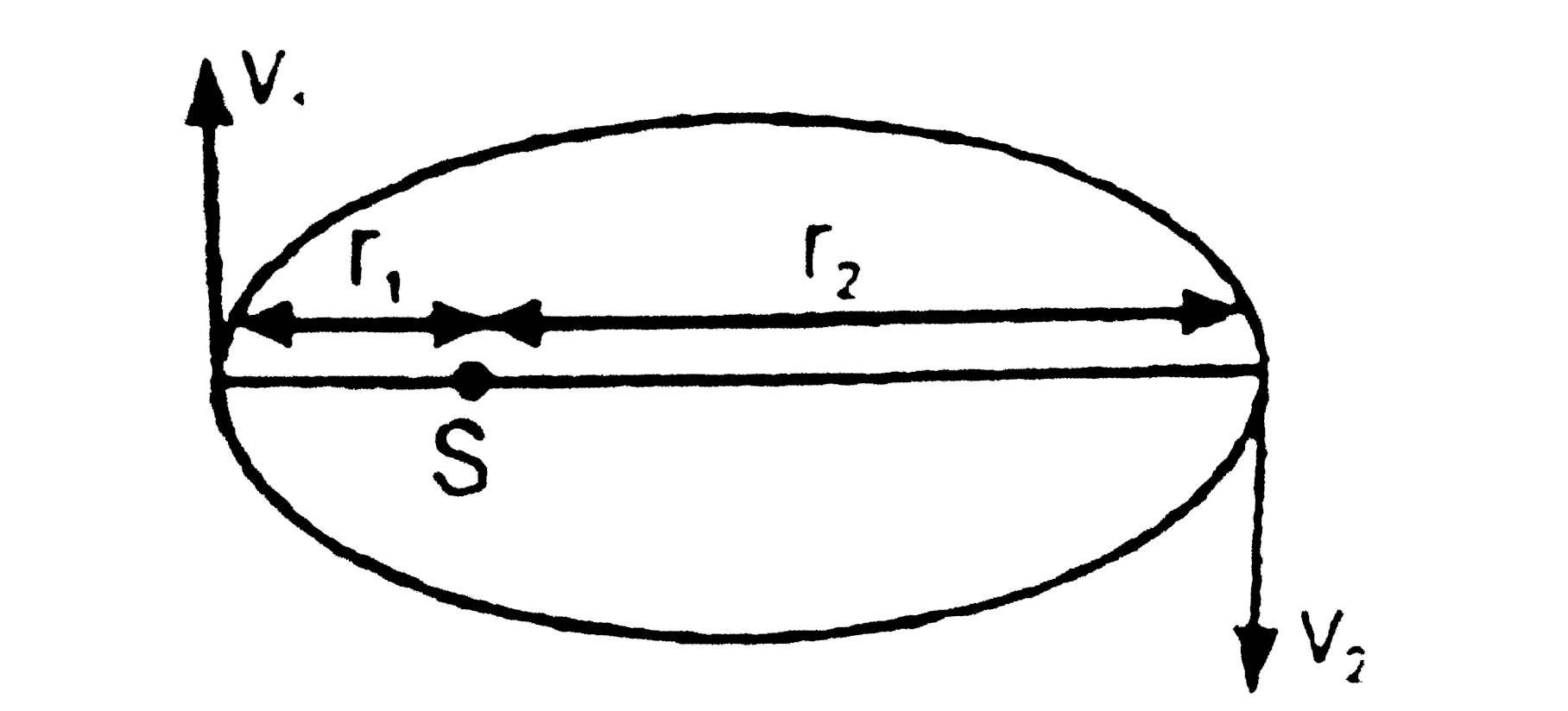
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
View Solution
