A particle A has chrage +q and a particle B has charge +4q with each of them having the same mass m. When allowed to fall from rest through the same electric potential difference, the ratio of their speed vAvB will become
2:1
1:2
1:4
4:1
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the electric potential difference, the charge of the particles, and their resulting speeds after falling through that potential difference.
1. Understand the Energy Conversion:
When a charged particle falls through an electric potential difference V, it converts electric potential energy into kinetic energy. The kinetic energy K gained by a particle is given by:
K=12mv2
where m is the mass of the particle and v is its final speed.
2. Electric Potential Energy:
The electric potential energy U gained by a charged particle when it falls through a potential difference V is given by:
U=qV
where q is the charge of the particle.
3. Setting Up the Equation:
For both particles A and B, we can set up the equations for kinetic energy:
- For particle A:
12mv2A=qV
- For particle B:
12mv2B=4qV
4. Solving for Speeds:
Rearranging both equations to solve for vA and vB:
- For particle A:
v2A=2qVm⟹vA=√2qVm
- For particle B:
v2B=8qVm⟹vB=√8qVm=√8√qVm=2√2√qVm
5. Finding the Ratio of Speeds:
Now, we can find the ratio of the speeds vAvB:
vAvB=√2qVm2√2√qVm
Simplifying this:
vAvB=√22√2=12
6. Final Result:
Thus, the ratio of their speeds is:
vAvB=12
Conclusion:
The ratio of the speeds of particles A and B is 12.
When a charged particle falls through an electric potential difference V, it converts electric potential energy into kinetic energy. The kinetic energy K gained by a particle is given by:
K=12mv2
where m is the mass of the particle and v is its final speed.
The electric potential energy U gained by a charged particle when it falls through a potential difference V is given by:
U=qV
where q is the charge of the particle.
For both particles A and B, we can set up the equations for kinetic energy:
- For particle A:
12mv2A=qV
- For particle B:
12mv2B=4qV
Rearranging both equations to solve for vA and vB:
- For particle A:
v2A=2qVm⟹vA=√2qVm
- For particle B:
v2B=8qVm⟹vB=√8qVm=√8√qVm=2√2√qVm
Now, we can find the ratio of the speeds vAvB:
vAvB=√2qVm2√2√qVm
Simplifying this:
vAvB=√22√2=12
Thus, the ratio of their speeds is:
vAvB=12
The ratio of the speeds of particles A and B is 12.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An α-particle and a proton are accelerated from rest through the same potential difference V. Find the ratio of de-Broglie wavelength associated with them.
View SolutionAn electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionAn electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionThe ratio of the deBroglie wavelengths of proton, deuteron and alpha particle accelerated through the same potential difference 100V is
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionIf λ1 and λ2 denote the de-Broglie wavelength of two particles with same masses but charges in the ratio of 1:2 after they are accelerated from rest through the same potential difference, then
View SolutionAn α - particle and a proton are accelerated through same potential difference. Find the ratio (va/vp) of velocities acquired by two particles.
View SolutionFigure shows two rings having charges Q and −√5Q. Find potential difference a and B i.e. (VA−VB).
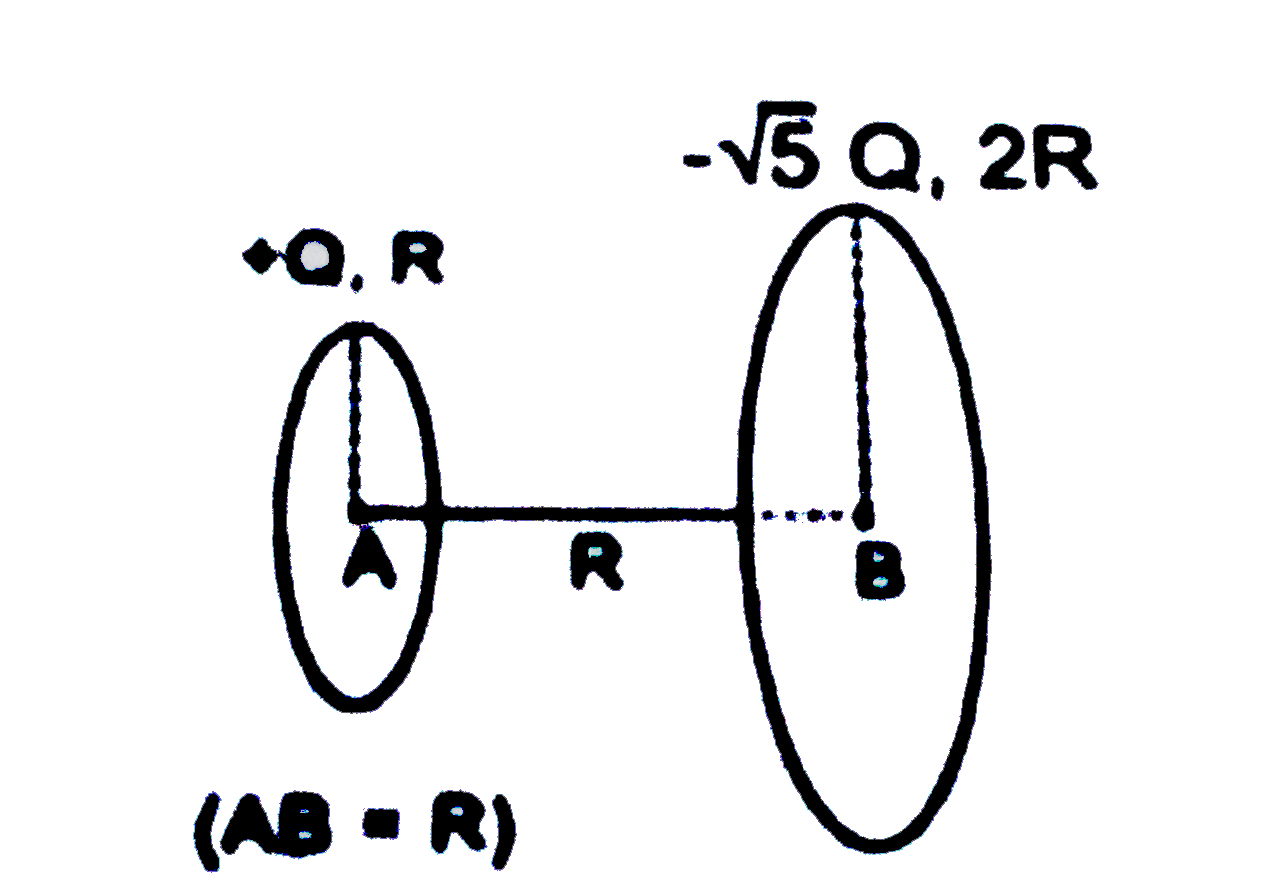
View SolutionMention the significance of Davisson-Germer experiment. An α-particle and a proton are accelerated from rest through the same potential difference V. Find the ratio of de-Broglie wavelengths associated with them.
View SolutionA proton and an α− Particle ( with their masses in the ratio of 1:4 and charges in the ratio of 1:2 ) are accelerated form rest through a potential differeence V, if a uniform magnetic field (B) is set up perpendicular to their velocities , the ratio of the radii rp:rα of the circular paths described by them will be :
View Solution