The electrostatic potential energy between proton and electron separated by a distance 1 Å is
13.6 eV
27.2 eV
−14.4eV
1.44 eV
The correct Answer is:C
To find the electrostatic potential energy (U) between a proton and an electron separated by a distance of 1 Å (angstrom), we can use the formula for electrostatic potential energy:
U=k⋅q1⋅q2r
where:
- U is the electrostatic potential energy,
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the charges of the proton and electron, respectively,
- r is the separation distance between the charges.
Step 1: Identify the charges
The charge of a proton (q1) is +1.6×10−19C and the charge of an electron (q2) is −1.6×10−19C.
Step 2: Convert the distance
The distance r is given as 1 Å, which is equal to 1×10−10m.
Step 3: Substitute the values into the formula
Now, substituting the values into the formula:
U=(9×109)⋅(1.6×10−19)⋅(−1.6×10−19)1×10−10
Step 4: Calculate the numerator
Calculating the numerator:
9×109⋅1.6×10−19⋅(−1.6×10−19)=9×109⋅(−2.56×10−38)=−23.04×10−29
Step 5: Divide by the distance
Now, divide by r:
U=−23.04×10−291×10−10=−23.04×10−19J
Step 6: Convert to electron volts
To convert joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
U=−23.04×10−191.6×10−19≈−14.4eV
Final Answer
The electrostatic potential energy between a proton and an electron separated by a distance of 1 Å is approximately −14.4eV.
---
- U is the electrostatic potential energy,
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the charges of the proton and electron, respectively,
- r is the separation distance between the charges.
The charge of a proton (q1) is +1.6×10−19C and the charge of an electron (q2) is −1.6×10−19C.
The distance r is given as 1 Å, which is equal to 1×10−10m.
Now, substituting the values into the formula:
Calculating the numerator:
Now, divide by r:
To convert joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
The electrostatic potential energy between a proton and an electron separated by a distance of 1 Å is approximately −14.4eV.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The force between two electrons separated by a distance r varies as
View SolutionThe mutual electrostatic potential energy between two protons which are at a distance of 9×10−15m, in .92U235 nucleus is
View SolutionThe force between two electrons separated by a distance r is proportional to
View SolutionFind out the value of electrostatic potential eneryg of two electrons separated by 3.0Å in vacuum. Express your answer in joules and electron volt.
View SolutionThe ratio of electrostatic and gravitational force acting between electron and proton separated by a distance 5×10−11m, will be (charge on electron =1.6×10−19C, mass of electron =9.1×10−31kg, mass of proton =1.6×10−27kg,G=6.7×10−11N−m2/kg2)
View SolutionThe electrostatic potential energy between two identical nuclei produced in the fission on of .23892U at the moment of their separation is x then find x/180. Given R0=1.3×10−15m and ε0=8.85×10−12Fm−1.
View SolutionA : Uncertainty principle demands that an electron confined to a nucleus must have very high energy so that the electron cannot reside in a nucleus.
R: The electrostatic attraction between electron and proton is large at such a small distance but is not enough to bind such a high -energy electron.
View SolutionSuppose the potential energy between an electron and a proton at a distance r is given by Ke2/3r3. Application of Bohr's theory tohydrogen atom in this case showns that
View SolutionFind the electrostatic potential energy of the system shown in the figure
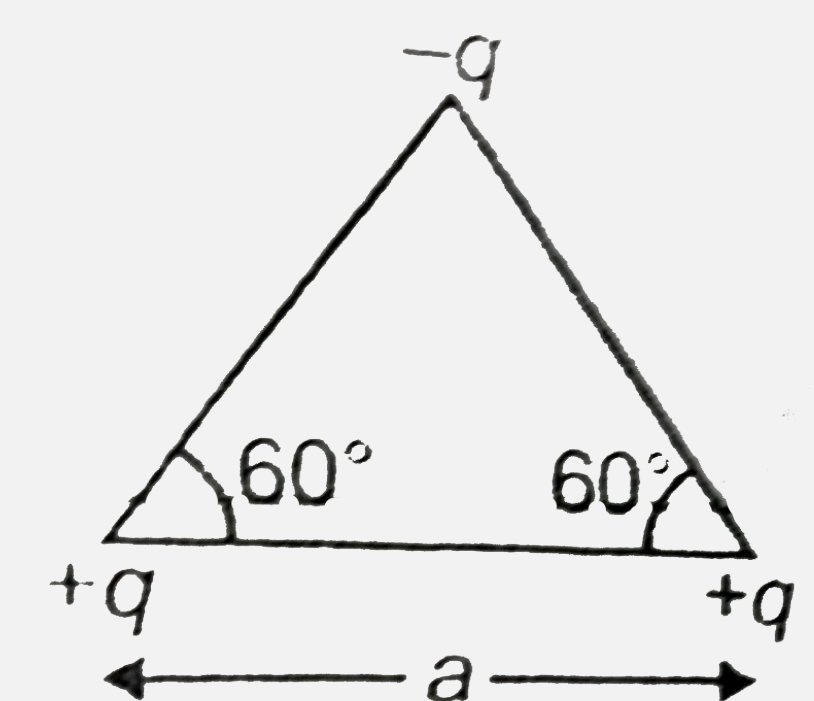
View SolutionFind the separation between two electron (inÅ) in vacuum, if electrostatic potential energy between these electrons in 7.67×10−19)J.
[Given: e= 1.6×10−19C ∈o=8.85×10−12 J^(-1)C^(2)m^(-1)π=3.14]
View Solution
