The electrostatic potential energy between two identical nuclei produced in the fission on of .23892U at the moment of their separation is x then find x/180. Given R0=1.3×10−15m and ε0=8.85×10−12Fm−1.
The correct Answer is:3
To solve the problem of calculating the electrostatic potential energy between two identical nuclei produced in the fission of 23892U, we will follow these steps:
Step 1: Determine the Charge of Each Nucleus
The charge of a nucleus is given by the formula:
Q=Z⋅e
where Z is the atomic number and e is the elementary charge (e=1.6×10−19C).
For uranium, the atomic number Z=92. After fission, each nucleus will have:
Z′=922=46
Thus, the charge of each nucleus is:
Q=46⋅(1.6×10−19)=7.36×10−18C
Step 2: Calculate the Radius of Each Nucleus
The radius of a nucleus can be estimated using the formula:
R=R0⋅A1/3
where R0=1.3×10−15m and A is the mass number.
For each nucleus after fission, the mass number is:
A′=2382=119
Thus, the radius is:
R=1.3×10−15⋅(119)1/3
Calculating (119)1/3:
(119)1/3≈4.92
So,
R≈1.3×10−15⋅4.92≈6.396×10−15m
Step 3: Calculate the Distance Between the Two Nuclei
Since we are considering the separation at the moment they are just about to separate, the distance d between the two nuclei is:
d=2R≈2⋅6.396×10−15≈1.2792×10−14m
Step 4: Calculate the Electrostatic Potential Energy
The electrostatic potential energy U between two point charges is given by:
U=k⋅Q1⋅Q2d
where k is Coulomb's constant (k=9×109N⋅m2/C2).
Since Q1=Q2=Q:
U=k⋅Q2d
Substituting the values:
U=9×109⋅(7.36×10−18)21.2792×10−14
Calculating (7.36×10−18)2:
(7.36×10−18)2≈5.41×10−35
Now substituting:
U≈9×109⋅5.41×10−351.2792×10−14≈4.87×10−251.2792×10−14≈3.81×10−11J
Step 5: Convert to Electron Volts
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
U≈3.81×10−111.6×10−19≈238.125MeV
Step 6: Calculate x180
Now we need to find x180:
x180=238.125180≈1.322
Final Answer
Thus, the value of x180 is approximately:
1.322
The charge of a nucleus is given by the formula:
Q=Z⋅e
where Z is the atomic number and e is the elementary charge (e=1.6×10−19C).
Z′=922=46
Thus, the charge of each nucleus is:
Q=46⋅(1.6×10−19)=7.36×10−18C
The radius of a nucleus can be estimated using the formula:
R=R0⋅A1/3
where R0=1.3×10−15m and A is the mass number.
A′=2382=119
Thus, the radius is:
R=1.3×10−15⋅(119)1/3
Calculating (119)1/3:
(119)1/3≈4.92
So,
R≈1.3×10−15⋅4.92≈6.396×10−15m
Since we are considering the separation at the moment they are just about to separate, the distance d between the two nuclei is:
d=2R≈2⋅6.396×10−15≈1.2792×10−14m
The electrostatic potential energy U between two point charges is given by:
U=k⋅Q1⋅Q2d
where k is Coulomb's constant (k=9×109N⋅m2/C2).
U=k⋅Q2d
Substituting the values:
U=9×109⋅(7.36×10−18)21.2792×10−14
Calculating (7.36×10−18)2:
(7.36×10−18)2≈5.41×10−35
Now substituting:
U≈9×109⋅5.41×10−351.2792×10−14≈4.87×10−251.2792×10−14≈3.81×10−11J
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
U≈3.81×10−111.6×10−19≈238.125MeV
Now we need to find x180:
x180=238.125180≈1.322
Thus, the value of x180 is approximately:
1.322
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-2 Part-3 One more than one options correct type
7 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-2 Part-4 Comprehension
6 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 2 Part-1 Only one option correct type
20 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
- REVISION DPPBOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions
463 Videos
Similar Questions
The mutual electrostatic potential energy between two protons which are at a distance of 9×10−15m, in .92U235 nucleus is
View SolutionFind the separation between two electron (inÅ) in vacuum, if electrostatic potential energy between these electrons in 7.67×10−19)J.
[Given: e= 1.6×10−19C ∈o=8.85×10−12 J^(-1)C^(2)m^(-1)π=3.14]
View Solution
Knowledge Check
If 200MeV energy is released in the fission of a single U235 nucleus, the number of fissions required per second to produce 1 kilowatt power shall be (Given 1eV=1.6×10−19J).
A3.125×1013B1.52×106C3.125×1012D3.125×1014
the radius of 29Cu64 nucleus in fermi is
(given ,r01.2×10−15M)
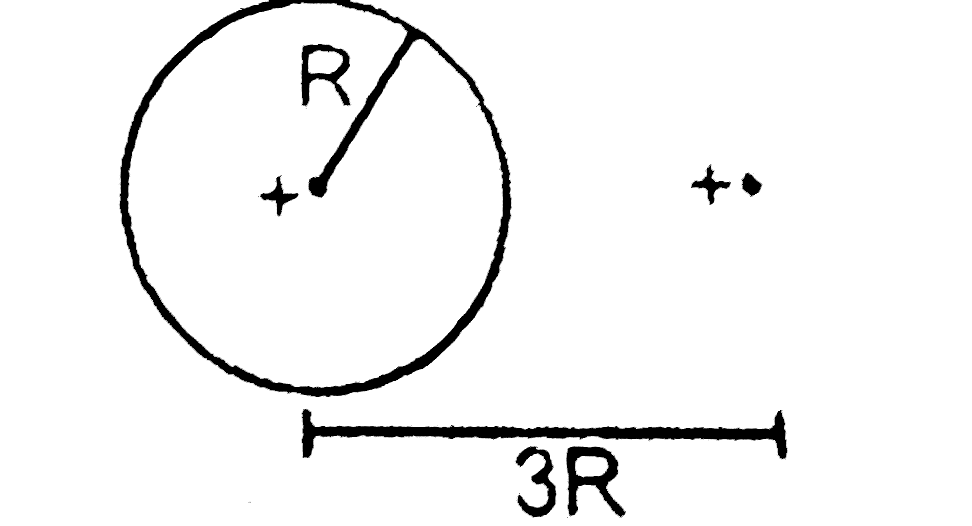
View SolutionFind the flux of the electric field through a spherical surface of radius R due to a charge of 8.85×10−8C at the centre and another equal charge at a point 3R away from the centre (Given : ε0=8.85×10−12 units )
View SolutionThe electrostatic potential existing in the space is given as V=−(x36ε0+2) volts. Find the charge density (in coulomb/m3) at x=2m.
View SolutionThe arrangement of parallel conducting plates shown in are of the same surgface area A=10cm2. A battery of E=10V is connected aross the kends A and B. Plate 2 is slowly moved upward by some exteral force.
 .
.
find the position of plate at which the energy stored in the system is minimum. Also, find this mimimum energy Take ε0=8.8×10−12Fm−1.
View Solution(A) Find the radius of nucleus of an atom having atomic mass number equal to 125.(TakeR0=1.3×10−15m)
View SolutionCalculate the energy released by the fission 1 g of .235U in joule, given that the energy released per fission is 200 MeV. (Avogadro.s number =6.023×1023 )
View SolutionFind the density of .126C nucleus. Take atomic mass of .126C as 12.00amu Take R0=1.2×10−15m .
View Solution