A capacitor when filled with a dielectric K=3 has charge Q0, voltage V0 and filed E0. If the dielectric is replaced with another one having K=9 the new values of charge, voltage and field will be respectively
3Q0,3V0,3E0
Q0,3V0,3E0
Q0,V03,3E0
Q0,V03,E03
The correct Answer is:D
To solve the problem, we need to analyze the changes in the capacitor's properties when the dielectric material is changed from K=3 to K=9. We will denote the initial values with subscript 0 and the new values with subscript 1.
1. Understanding the Relationship Between Charge, Voltage, and Capacitance:
The charge Q on a capacitor is given by the formula:
Q=C⋅V
where C is the capacitance and V is the voltage across the capacitor.
2. Capacitance with Dielectric:
The capacitance of a capacitor filled with a dielectric material is given by:
C=K⋅C0
where K is the dielectric constant and C0 is the capacitance without the dielectric.
3. Initial Conditions:
For the initial dielectric with K=3:
C0=C0(initialcapacitance)
C1=3⋅C0(newcapacitancewithK=3)
The initial charge and voltage are:
Q0=C0⋅V0
4. New Conditions with Dielectric K=9:
When the dielectric is replaced with one having K=9:
C2=9⋅C0(newcapacitancewithK=9)
5. Charge Conservation:
Since there is no battery connected, the charge remains constant:
Q1=Q0
6. Finding New Voltage V1:
Using the charge conservation:
Q1=C2⋅V1
Substituting Q0 for Q1:
Q0=(9⋅C0)⋅V1
Now substituting Q0=C0⋅V0:
C0⋅V0=(9⋅C0)⋅V1
Dividing both sides by C0 (assuming C0≠0):
V0=9⋅V1
Thus,
V1=V09
7. Finding New Electric Field E1:
The electric field E is related to voltage and distance d by:
E=Vd
Since the distance d remains constant, the electric field will change proportionally to the voltage:
E1=V1d=V0/9d=E09
Final Results:
- New Charge Q1=Q0
- New Voltage V1=V09
- New Electric Field E1=E09
Summary:
The new values of charge, voltage, and electric field when the dielectric is replaced with K=9 are:
- Charge: Q1=Q0
- Voltage: V1=V09
- Electric Field: E1=E09
The charge Q on a capacitor is given by the formula:
Q=C⋅V
where C is the capacitance and V is the voltage across the capacitor.
The capacitance of a capacitor filled with a dielectric material is given by:
C=K⋅C0
where K is the dielectric constant and C0 is the capacitance without the dielectric.
For the initial dielectric with K=3:
C0=C0(initialcapacitance)
C1=3⋅C0(newcapacitancewithK=3)
The initial charge and voltage are:
Q0=C0⋅V0
When the dielectric is replaced with one having K=9:
C2=9⋅C0(newcapacitancewithK=9)
Since there is no battery connected, the charge remains constant:
Q1=Q0
Using the charge conservation:
Q1=C2⋅V1
Substituting Q0 for Q1:
Q0=(9⋅C0)⋅V1
Now substituting Q0=C0⋅V0:
C0⋅V0=(9⋅C0)⋅V1
Dividing both sides by C0 (assuming C0≠0):
V0=9⋅V1
Thus,
V1=V09
The electric field E is related to voltage and distance d by:
E=Vd
Since the distance d remains constant, the electric field will change proportionally to the voltage:
E1=V1d=V0/9d=E09
- New Charge Q1=Q0
- New Voltage V1=V09
- New Electric Field E1=E09
The new values of charge, voltage, and electric field when the dielectric is replaced with K=9 are:
- Charge: Q1=Q0
- Voltage: V1=V09
- Electric Field: E1=E09
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.

View SolutionAn isolated capacitor of capacitance C is charged to a potential V. Then a dielectric slab of dielectric constant K is inserted as shown. The net charge on four surfaces 1,2, 3 and 4 would be respectively.

View SolutionA parallel - plate capacitor, filled with a dielectric of dielectric constant k, is charged to a potential V0. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant τ, through a resistance, then find time after which the potential difference across it will be V0?
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

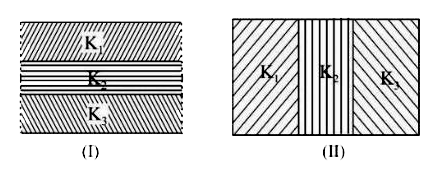
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3.
The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II.
If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be ( E1 refers to capacitor (I) and E2 to capacitor (II)):
View SolutionA parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
View SolutionA parallel plate capacitor without any dielectric has capacitance C0. A dielectric slab is made up of two dielectric slabs of dielectric constants K and 2K and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric K enters first) in between the plates at constant speed, then variation of capacitance with time will be best represented by :

View SolutionA capacitor is connected to a battery of voltage V. Now a di-electric slab of di-electric constant k is completely inserted between the plates, then the final charge on the capacitor will be : (If initial charge is q0)
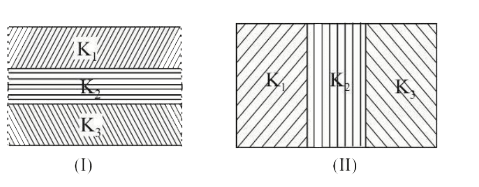
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
View Solution
