A parallel plate capacitor of capacitance C is connected to a battery and is charged to a potential difference V. Another capacitor of capacitance 2C is ismilarly charged to a potential difference 2V. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the poistive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
zero
25CV26
3CV22
9CV22
The correct Answer is:C
To find the final energy of the configuration when two capacitors are connected in parallel with opposite polarity, we can follow these steps:
1. Calculate the Initial Charges:
- For the first capacitor (capacitance C and voltage V):
Q1=C⋅V
- For the second capacitor (capacitance 2C and voltage 2V):
Q2=2C⋅2V=4CV
2. Determine the Net Charge:
- When the two capacitors are connected in parallel with opposite polarity, the net charge Qnet is given by:
Qnet=Q1−Q2=CV−4CV=−3CV
- The negative sign indicates that the net charge is in the direction of the larger charge.
3. Calculate the Equivalent Capacitance:
- The equivalent capacitance Ceq when capacitors are connected in parallel is the sum of their capacitances:
Ceq=C+2C=3C
4. Find the Final Voltage:
- The final voltage Vf across the equivalent capacitance can be calculated using the formula:
Vf=QnetCeq=−3CV3C=−V
- The negative sign indicates that the voltage is in the opposite direction to the initial voltage.
5. Calculate the Final Energy:
- The energy U stored in the capacitors can be calculated using the formula:
U=Q2net2Ceq
- Substituting the values we have:
U=(−3CV)22⋅3C=9C2V26C=32CV2
Final Answer:
The final energy of the configuration is:
32CV2
- For the first capacitor (capacitance C and voltage V):
Q1=C⋅V
- For the second capacitor (capacitance 2C and voltage 2V):
Q2=2C⋅2V=4CV
- When the two capacitors are connected in parallel with opposite polarity, the net charge Qnet is given by:
Qnet=Q1−Q2=CV−4CV=−3CV
- The negative sign indicates that the net charge is in the direction of the larger charge.
- The equivalent capacitance Ceq when capacitors are connected in parallel is the sum of their capacitances:
Ceq=C+2C=3C
- The final voltage Vf across the equivalent capacitance can be calculated using the formula:
Vf=QnetCeq=−3CV3C=−V
- The negative sign indicates that the voltage is in the opposite direction to the initial voltage.
- The energy U stored in the capacitors can be calculated using the formula:
U=Q2net2Ceq
- Substituting the values we have:
U=(−3CV)22⋅3C=9C2V26C=32CV2
The final energy of the configuration is:
32CV2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(B) Chapter exercises
Explore 17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:Check point 2.5
Explore 20 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Medical entrances gallery
Explore 37 Videos
Similar Questions
A capacitor of capacity C is charged to a potential difference V and another capacitor of capacity 2C is charged to a potential difference 4V. The charged batteries are disconnected and the two capacitors are connected with reverse polarity (i.e. positive plate of first capacitor is connected to negative plate of second capacitor). The heat produced during the redistribution of charge between the capacitors will be
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1Two idential capacitors are joined in parallel, charged to a potential V and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
AThe charges on the free plated connected together are destoyed.BThe energy stored in the system increases.CThe potential difference between the free plates is 2V.DThe potential difference remains constant.
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
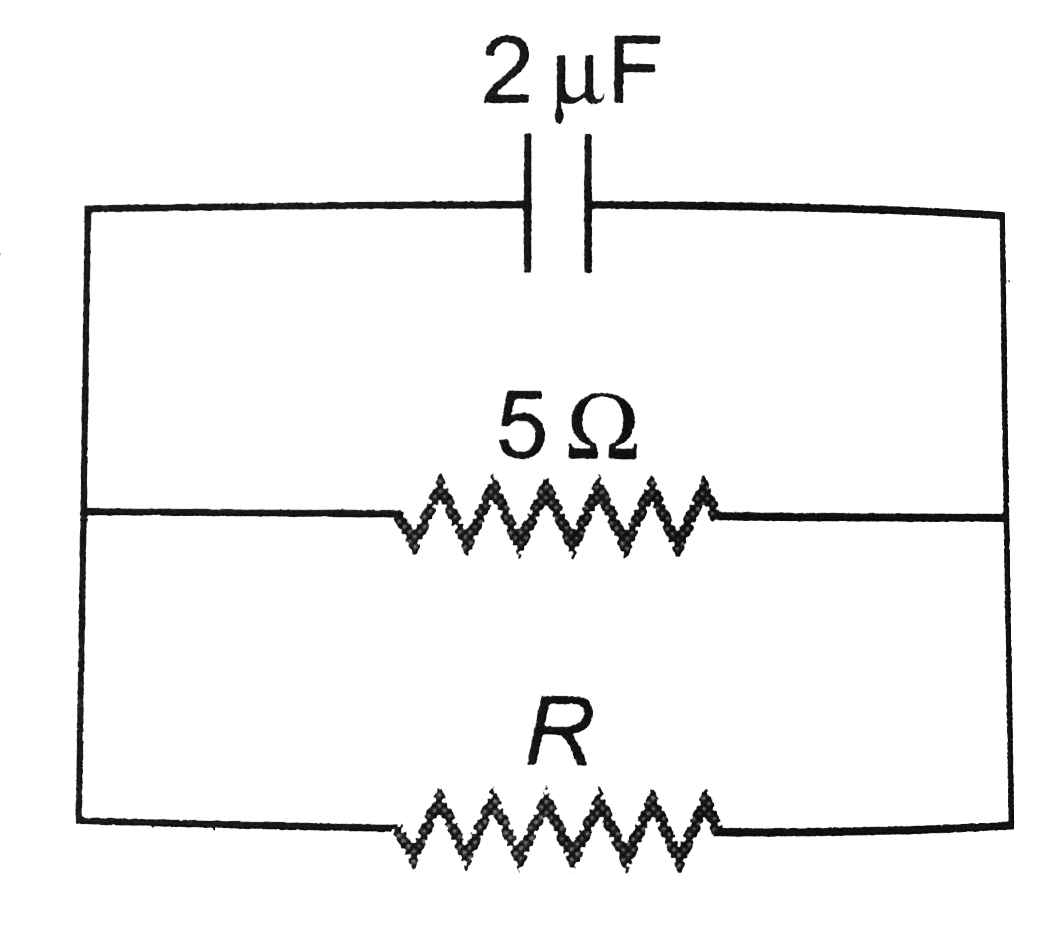
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to

View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitance C which is initially charged up to a potential differnce ε is connected with a battery of emf ε2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. Find the heat loss in the circuit the process of charging.
View Solution