The potential of a large liquid drop when eight liquid drops are combined is 20 V. Then, the potential of each single drop was
10 V
7.5 V
5 V
2.5 V
The correct Answer is:A
To find the potential of each single drop when eight liquid drops are combined to form a larger drop with a potential of 20 V, we can follow these steps:
Step 1: Understand the potential of a single drop
The potential V of a single drop (small sphere) with charge Q and radius r is given by the formula:
V=kQr
where k is the electrostatic constant.
Step 2: Combine the drops
When eight such drops are combined, the total charge of the larger drop becomes:
Qtotal=8Q
The radius of the larger drop R can be determined from the volume conservation principle. The volume of a sphere is given by:
V=43πr3
Thus, the volume of eight small drops is:
Vsmall=8×43πr3=323πr3
The volume of the larger drop is:
Vlarge=43πR3
Setting these equal gives:
323πr3=43πR3
Cancelling 43π from both sides:
32r3=R3
Taking the cube root:
R=2r
Step 3: Calculate the potential of the larger drop
The potential VB of the larger drop is given as 20 V. The potential of the larger drop can also be expressed as:
VB=kQtotalR=k(8Q)R
Substituting R=2r:
VB=k(8Q)2r=4kQr
Step 4: Relate the potentials
From the earlier equation for the potential of a single drop:
V=kQr
We can express the potential of the larger drop in terms of the potential of a single drop:
VB=4V
Step 5: Solve for the potential of a single drop
Given VB=20 V, we can find V:
20=4V⟹V=204=5 V
Final Answer
Thus, the potential of each single drop is:
5 V
The potential V of a single drop (small sphere) with charge Q and radius r is given by the formula:
V=kQr
where k is the electrostatic constant.
When eight such drops are combined, the total charge of the larger drop becomes:
Qtotal=8Q
The radius of the larger drop R can be determined from the volume conservation principle. The volume of a sphere is given by:
V=43πr3
Thus, the volume of eight small drops is:
Vsmall=8×43πr3=323πr3
The volume of the larger drop is:
Vlarge=43πR3
Setting these equal gives:
323πr3=43πR3
Cancelling 43π from both sides:
32r3=R3
Taking the cube root:
R=2r
The potential VB of the larger drop is given as 20 V. The potential of the larger drop can also be expressed as:
VB=kQtotalR=k(8Q)R
Substituting R=2r:
VB=k(8Q)2r=4kQr
From the earlier equation for the potential of a single drop:
V=kQr
We can express the potential of the larger drop in terms of the potential of a single drop:
VB=4V
Given VB=20 V, we can find V:
20=4V⟹V=204=5 V
Thus, the potential of each single drop is:
5 V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Why are falling liquid drops spherical?
View SolutionWhy are falling liquid drops spherical?
View SolutionA spherical drop of capacitance 1μF is broken into eight drop of equal radius. Then, the capacitance of each small drop is
View SolutionEight oil drops of same size are charged to a potential to 50 V each. These oil drops are merged into one single larged drop. What will be the potential of the large drop ?
View SolutionWhy is a liquid drop spherical in shape ?
View SolutionEight equals charged tiny drops are combined to form a big drop. If the potential on each drop is 10V then potential of big drop will be -
View SolutionA mercury drop has potential 'V' on its surface. 1000 such drops combine to form a new drop. Find the potential on the surface of the new drop.
View SolutionEight small drops, each of radius r and having same charge q are combined to form a big drop. The ratio between the potentials of the bigger drop and the smaller drop is
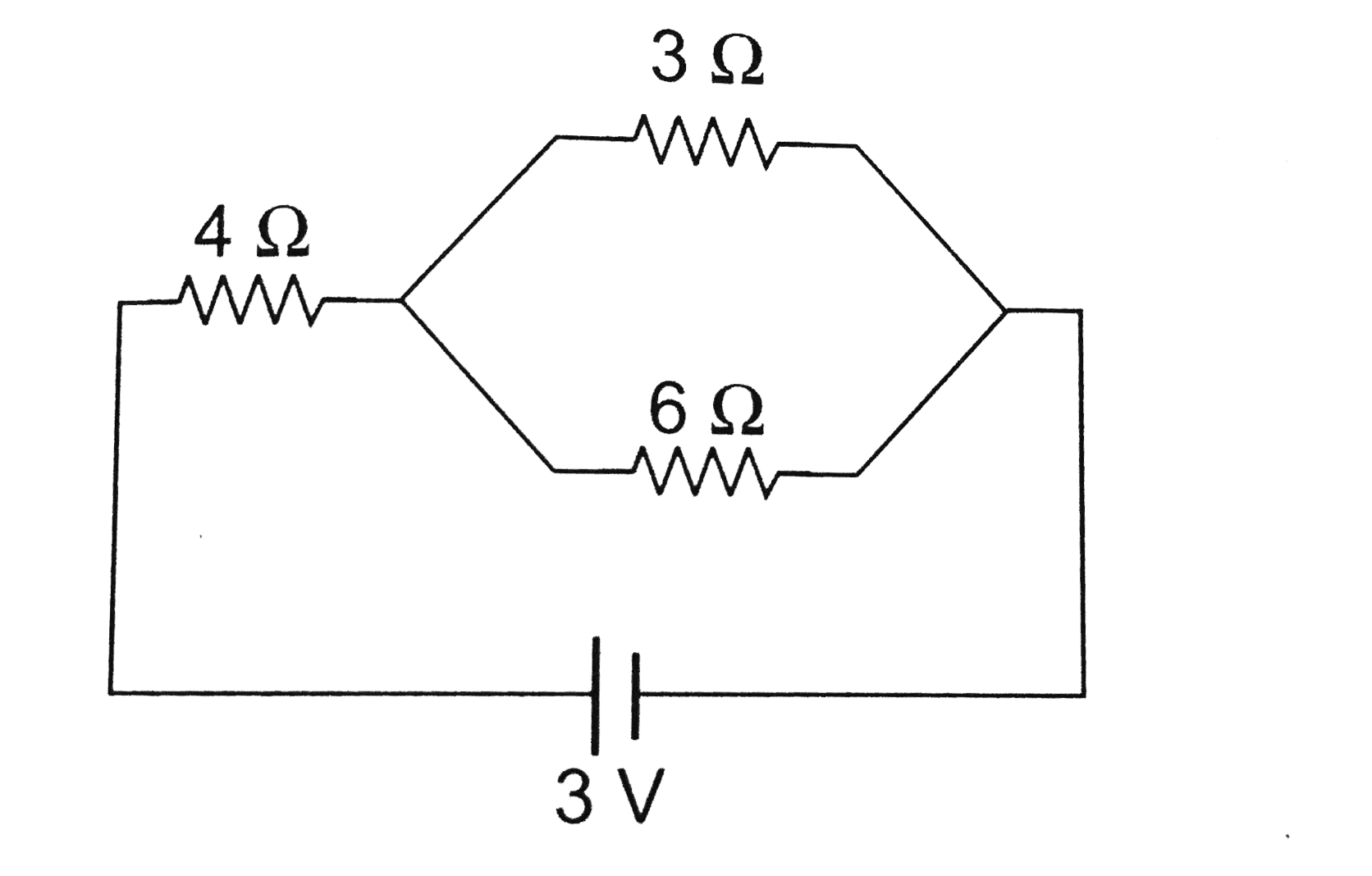
View SolutionThe potential drop across the 3Ω resistor is
View SolutionThe potential drop across 7μF capacitor is 6V. Then
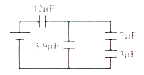
View Solution
