Two metal spheres of radii 0.01 m and 0.02 m are given a charge of 15 mC and 45 mC, respectively. They are then connected by a wire. The final charge on the first is …×10−3C.
40
30
20
10
The correct Answer is:C
To solve the problem step by step, we need to follow these logical steps:
Step 1: Understand the Problem
We have two metal spheres with given radii and charges. When they are connected by a wire, the charge will redistribute between them until they reach the same electric potential.
Step 2: Identify Given Values
- Radius of sphere 1, r1=0.01m
- Radius of sphere 2, r2=0.02m
- Charge on sphere 1, Q1=15mC=15×10−3C
- Charge on sphere 2, Q2=45mC=45×10−3C
Step 3: Charge Conservation
The total charge before connecting the spheres is equal to the total charge after they are connected:
Q1+Q2=Q′1+Q′2
where Q′1 and Q′2 are the final charges on spheres 1 and 2, respectively.
Calculating the total initial charge:
Qtotal=15×10−3+45×10−3=60×10−3C
Step 4: Equal Potential Condition
When the spheres are connected, they will have the same potential:
V1=V2
Using the formula for electric potential V=KQr, we can write:
KQ′1r1=KQ′2r2
Since K is a constant and can be canceled out, we have:
Q′1r1=Q′2r2
Step 5: Relate the Charges
From the above equation, we can express Q′2 in terms of Q′1:
Q′2=r2r1Q′1
Given that r1=0.01m and r2=0.02m:
r2r1=0.020.01=2
Thus, we have:
Q′2=2Q′1
Step 6: Substitute into Charge Conservation Equation
Now substitute Q′2 into the charge conservation equation:
Q′1+Q′2=60×10−3
Substituting Q′2=2Q′1:
Q′1+2Q′1=60×10−3
3Q′1=60×10−3
Q′1=60×10−33=20×10−3C
Step 7: Final Answer
The final charge on the first sphere is:
Q′1=20×10−3C
We have two metal spheres with given radii and charges. When they are connected by a wire, the charge will redistribute between them until they reach the same electric potential.
- Radius of sphere 1, r1=0.01m
- Radius of sphere 2, r2=0.02m
- Charge on sphere 1, Q1=15mC=15×10−3C
- Charge on sphere 2, Q2=45mC=45×10−3C
The total charge before connecting the spheres is equal to the total charge after they are connected:
Q1+Q2=Q′1+Q′2
where Q′1 and Q′2 are the final charges on spheres 1 and 2, respectively.
Qtotal=15×10−3+45×10−3=60×10−3C
When the spheres are connected, they will have the same potential:
V1=V2
Using the formula for electric potential V=KQr, we can write:
KQ′1r1=KQ′2r2
Since K is a constant and can be canceled out, we have:
Q′1r1=Q′2r2
From the above equation, we can express Q′2 in terms of Q′1:
Q′2=r2r1Q′1
Given that r1=0.01m and r2=0.02m:
r2r1=0.020.01=2
Thus, we have:
Q′2=2Q′1
Now substitute Q′2 into the charge conservation equation:
Q′1+Q′2=60×10−3
Substituting Q′2=2Q′1:
Q′1+2Q′1=60×10−3
3Q′1=60×10−3
Q′1=60×10−33=20×10−3C
The final charge on the first sphere is:
Q′1=20×10−3C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View Solution
Knowledge Check
A metallic sphere of radius 18 cm has been given a charge of 5×10−6C. The energy of the charged conductor is
A0.2JB0.6JC1.2JD2.4J
Two concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionThere are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
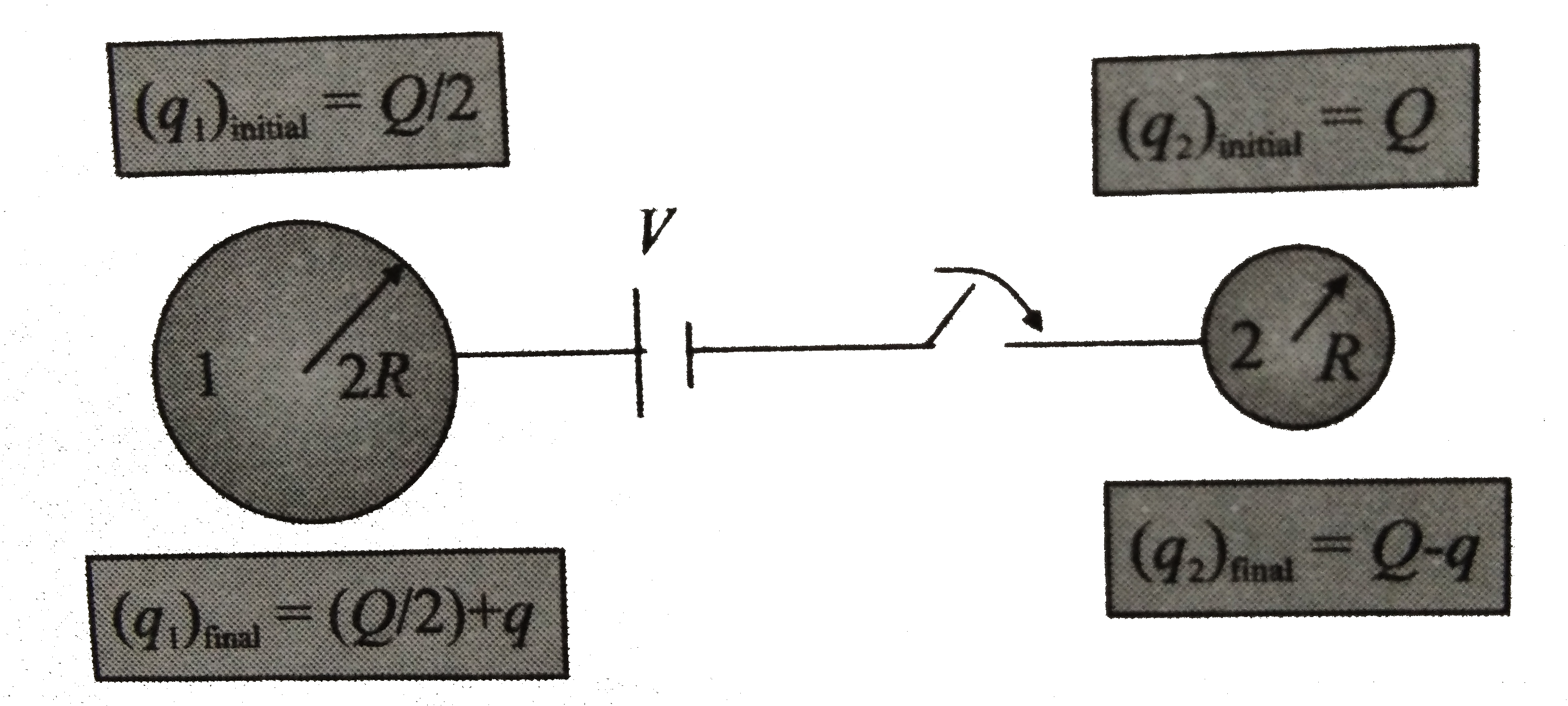
View SolutionFigure shows two conducting spheres separated by large distance and of radius 2 cm and 3 cm containing charges 10μC and 20μC respectively. When the spheres are connected by a conducting wire then find out following :
(i) Ratio of the final charge.
(ii) Final charge on each sphere.
(iii) Ratio of final charge densities.
(iv) Heat produced during the process.

View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionTwo insulated charges conducting spheres of radii 20 cm and 15 cm respectively and having an equal charge of 10μC are connected by a copper wire and then they are separated . Then
(1) Both spheres will have equal charges.
(2) Surface charges density on the 20 cm sphere will be greater than that on the 15 cm sphere
(3) Surface charge density on the 15 cm sphere will greater than that on the 20 cm sphere
(4) Surface charge density on the two spheres will be equal.
View SolutionTwo homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
View Solution
