A potentiometer wire has length 4m and resistance 8Ω. The resistance that must be connected in series with the wire and an accumulator of e.m.f. 2V, so as the get a potential gradient 1mV per cm on the wire is
32Ω
40Ω
44Ω
48Ω
The correct Answer is:A
To solve the problem, we need to determine the resistance that must be connected in series with a potentiometer wire to achieve a specific potential gradient. Let's break down the solution step by step.
Step 1: Understand the Problem
We have a potentiometer wire of length L=4m (which is 400cm) and resistance Rw=8Ω. We need to achieve a potential gradient of 1mV/cm using an accumulator with an EMF of 2V.
Step 2: Calculate the Total Voltage Drop Required
The potential gradient is given as 1mV/cm. To find the total voltage drop (ΔV) across the entire length of the wire, we multiply the potential gradient by the length of the wire in cm:
ΔV=Potential Gradient×Length=1mV/cm×400cm=400mV=0.4V
Step 3: Apply Ohm's Law
Using Ohm's Law, we know that the voltage drop across a resistor is given by:
ΔV=I×Rtotal
Where Rtotal is the total resistance in the circuit, which is the sum of the resistance of the wire and the series resistance Rs:
Rtotal=Rw+Rs=8Ω+Rs
Step 4: Calculate the Current
The current I can be expressed in terms of the EMF (V) and the total resistance:
I=VRtotal=2V8+Rs
Step 5: Substitute Current into Voltage Equation
Substituting the expression for current into the voltage equation gives:
0.4=(28+Rs)×(8)
Step 6: Solve for Rs
Now we can rearrange the equation to solve for Rs:
0.4=168+Rs
Cross-multiplying gives:
0.4(8+Rs)=16
Expanding this:
3.2+0.4Rs=16
Subtracting 3.2 from both sides:
0.4Rs=12.8
Dividing by 0.4:
Rs=12.80.4=32Ω
Conclusion
The resistance that must be connected in series with the wire is Rs=32Ω.
---
We have a potentiometer wire of length L=4m (which is 400cm) and resistance Rw=8Ω. We need to achieve a potential gradient of 1mV/cm using an accumulator with an EMF of 2V.
The potential gradient is given as 1mV/cm. To find the total voltage drop (ΔV) across the entire length of the wire, we multiply the potential gradient by the length of the wire in cm:
Using Ohm's Law, we know that the voltage drop across a resistor is given by:
The current I can be expressed in terms of the EMF (V) and the total resistance:
Substituting the expression for current into the voltage equation gives:
Now we can rearrange the equation to solve for Rs:
The resistance that must be connected in series with the wire is Rs=32Ω.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns4videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A potentiometer wire has length 5m and resistance 1002. A rheostat of range (1002−1k2) and accumulator of emf 20 V is connected with potentiometer wire. The maximum potential gradient possible in the wire is
View SolutionA potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View Solution
Knowledge Check
- Question 1 - Select One
The potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
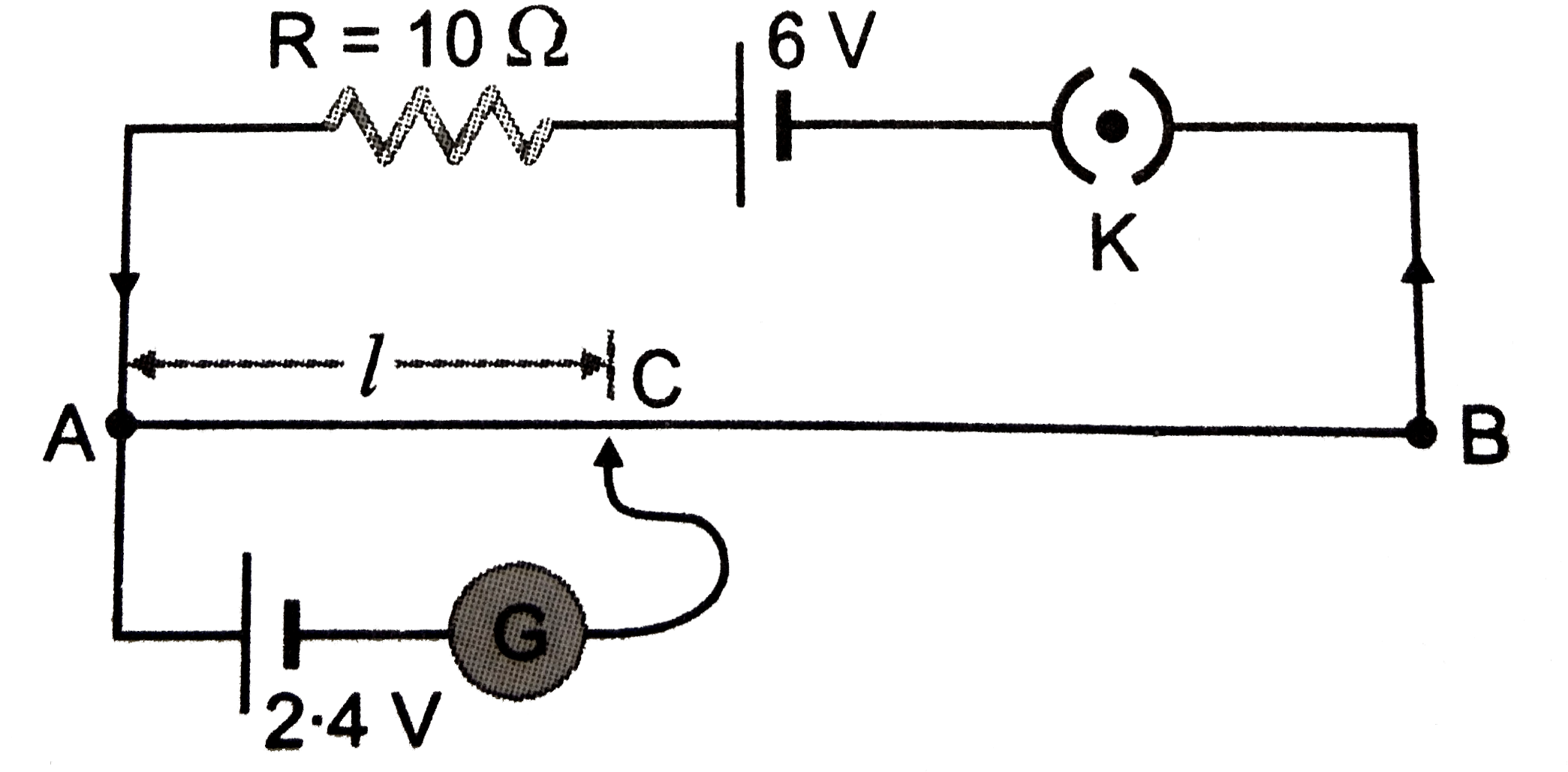 A100cmB120cmC110cmD140cm
A100cmB120cmC110cmD140cm - Question 2 - Select One
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090Ω
AB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
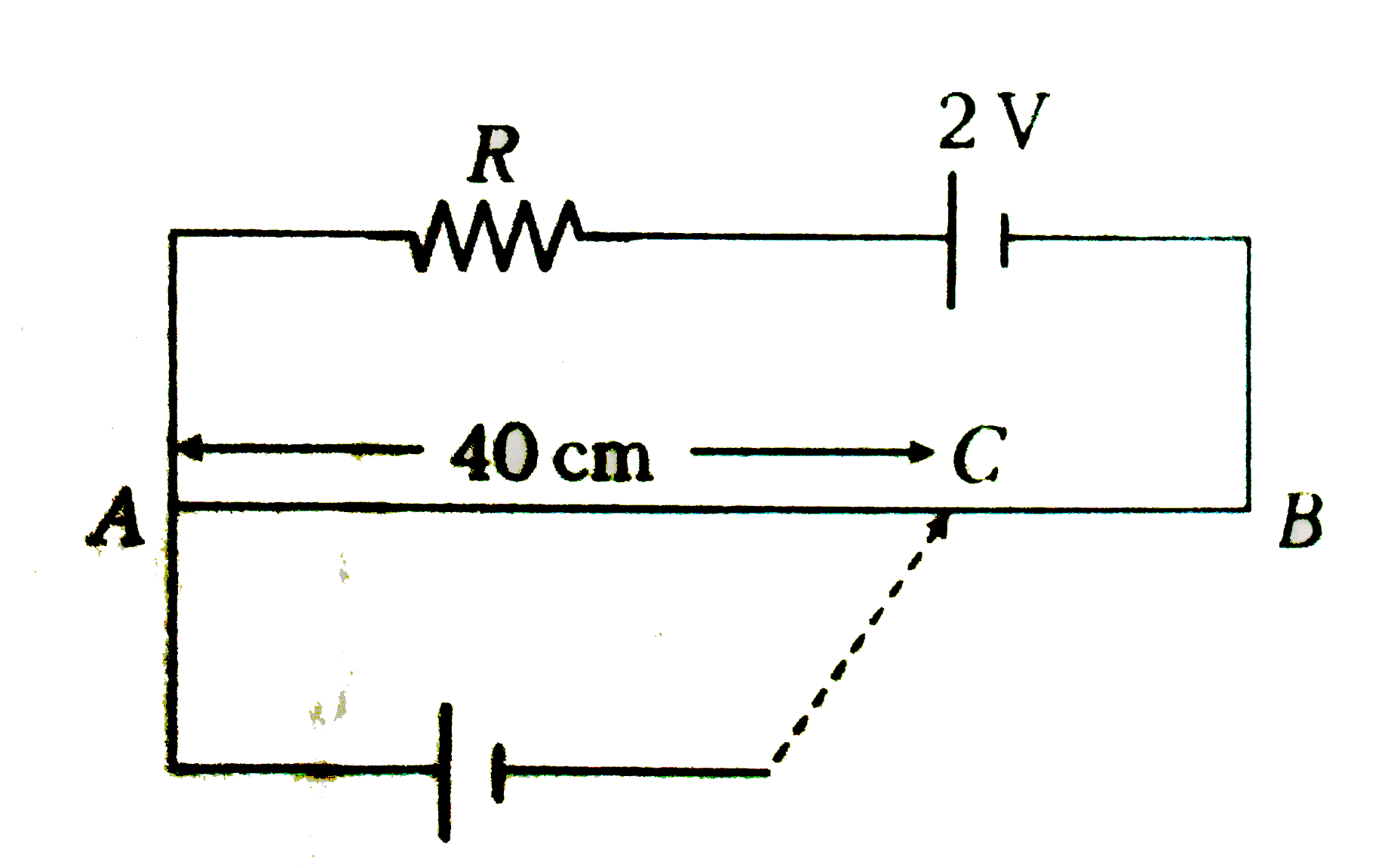 View Solution
View SolutionA potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R isView SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
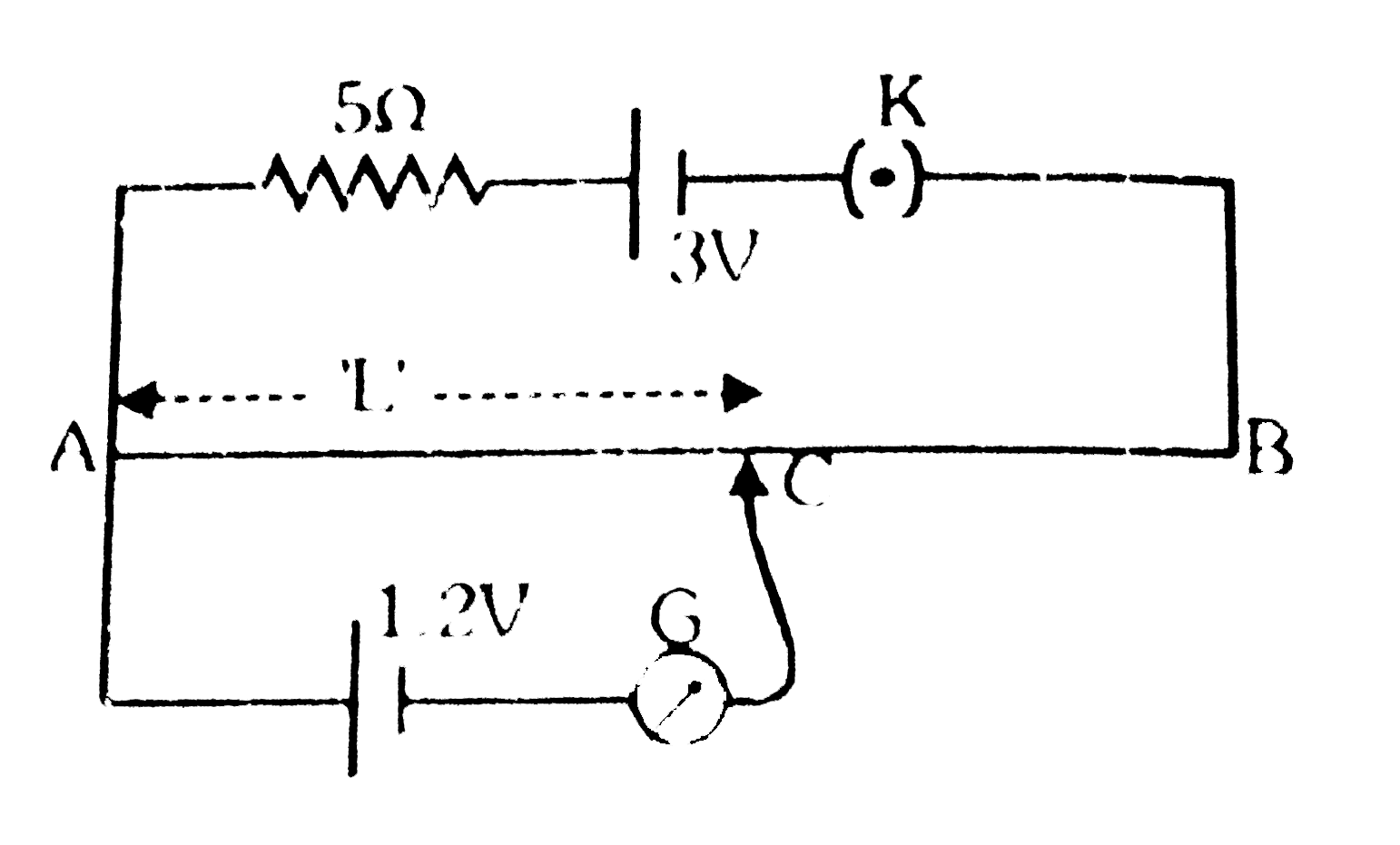 View Solution
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View SolutionThe emf of the driver cell of a potentiometer is 2V, and its internal resistance is negligible. The length of the potentiometer wire is 100cm, and resistance is 5ohm. How much resistance is to be connected in series with the potentiometer wire to have a potential gradient of 0.05mVcm−1?
View Solution

