Two wires of the same dimensions but resistivities and are connected in series. The equivalent resistivity of the combination is
The correct Answer is:A
To find the equivalent resistivity of two wires with resistivities p1 and p2 connected in series, we can follow these steps:
Step 1: Understand the Resistance of Each Wire
The resistance R of a wire is given by the formula:
R=p⋅LA
where:
- p is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
Step 2: Calculate the Resistance of Each Wire
For the first wire with resistivity p1:
R1=p1⋅LA
For the second wire with resistivity p2:
R2=p2⋅LA
Step 3: Find the Total Resistance in Series
When resistors are connected in series, the total resistance R is the sum of the individual resistances:
R=R1+R2=p1⋅LA+p2⋅LA
This can be simplified to:
R=(p1+p2)⋅LA
Step 4: Express the Total Resistance in Terms of Equivalent Resistivity
Now, we can express the total resistance R in terms of an equivalent resistivity p:
R=p⋅(2L)A
Here, we consider the two wires as a single wire of length 2L and the same cross-sectional area A.
Step 5: Set the Two Expressions for Resistance Equal
Setting the two expressions for resistance equal gives:
(p1+p2)⋅LA=p⋅(2L)A
Step 6: Simplify to Find Equivalent Resistivity
We can cancel L and A from both sides:
p1+p2=2p
Solving for p gives:
p=p1+p22
Conclusion
The equivalent resistivity p of the two wires connected in series is:
p=p1+p22
The resistance R of a wire is given by the formula:
R=p⋅LA
where:
- p is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
For the first wire with resistivity p1:
R1=p1⋅LA
R2=p2⋅LA
When resistors are connected in series, the total resistance R is the sum of the individual resistances:
R=R1+R2=p1⋅LA+p2⋅LA
This can be simplified to:
R=(p1+p2)⋅LA
Now, we can express the total resistance R in terms of an equivalent resistivity p:
R=p⋅(2L)A
Here, we consider the two wires as a single wire of length 2L and the same cross-sectional area A.
Setting the two expressions for resistance equal gives:
(p1+p2)⋅LA=p⋅(2L)A
We can cancel L and A from both sides:
p1+p2=2p
Solving for p gives:
p=p1+p22
The equivalent resistivity p of the two wires connected in series is:
p=p1+p22
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
Two resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
A(800±1)ΩB(800±7)ΩC(200±7)ΩD(200±1)Ω
The wire of same dimension but resistivities(p1) and (p2)are connected in parallel. The equivalent resistivity of the combination is
View SolutionThe wires is of same dimension but resistivities ρ1 and ρ2 are connected in parallel . The equivalent resistivity of the combination is
View SolutionThe equivalent resistance of the combination across AB is .
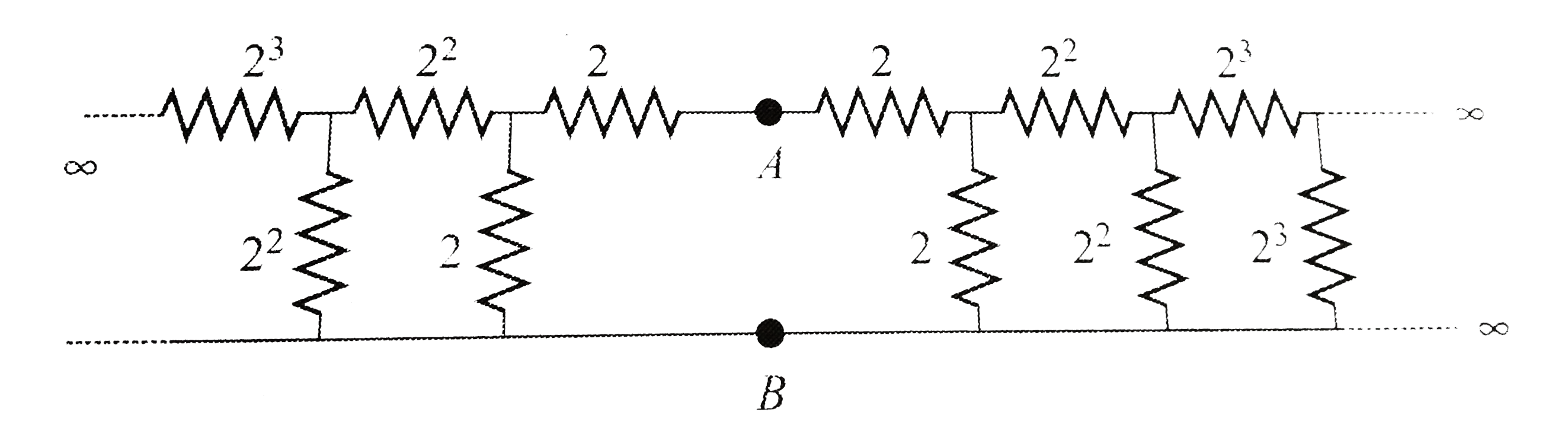
View SolutionTwo resistors of 2.092 and 3.0 22 are connected
in series. Find the effective resistance of combination .
View SolutionA wire of resistance R is cut into ‘ n ’ equal parts. These parts are then connected in parallel. The equivalent resistance of the combination will be
View SolutionThe resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View Solution
