A 0.8 m long solenoid has 800 turns and a field density of 2.52×10−3 T at its certre .Find the current in the solenoid
To find the current in the solenoid, we can use the formula for the magnetic field inside a solenoid, which is given by:
B=μ0⋅NL⋅I
Where:
- B is the magnetic field (in Tesla)
- μ0 is the permeability of free space (4π×10−7T m/A)
- N is the total number of turns
- L is the length of the solenoid (in meters)
- I is the current (in Amperes)
Step 1: Identify the given values
From the problem, we have:
- Length of the solenoid, L=0.8m
- Total number of turns, N=800
- Magnetic field at the center, B=2.52×10−3T
Step 2: Calculate the number of turns per unit length
The number of turns per unit length n can be calculated as:
n=NL=8000.8=1000turns/m
Step 3: Rearrange the formula to find the current I
We can rearrange the formula for the magnetic field to solve for the current I:
I=B⋅Lμ0⋅N
Step 4: Substitute the values into the equation
Now we can substitute the known values into the equation:
I=(2.52×10−3T)⋅(0.8m)(4π×10−7T m/A)⋅(800)
Step 5: Calculate the denominator
First, calculate the denominator:
μ0⋅N=(4π×10−7)⋅800
Calculating 4π:
4π≈12.5664
Thus,
μ0⋅N≈12.5664×10−7⋅800≈1.0053×10−3
Step 6: Substitute back and calculate I
Now substituting back into the equation for I:
I=(2.52×10−3)⋅(0.8)1.0053×10−3
Calculating the numerator:
2.52×10−3⋅0.8=2.016×10−3
Now divide:
I≈2.016×10−31.0053×10−3≈2.00A
Final Answer
The current in the solenoid is approximately 2.00A.
---
- B is the magnetic field (in Tesla)
- μ0 is the permeability of free space (4π×10−7T m/A)
- N is the total number of turns
- L is the length of the solenoid (in meters)
- I is the current (in Amperes)
From the problem, we have:
- Length of the solenoid, L=0.8m
- Total number of turns, N=800
- Magnetic field at the center, B=2.52×10−3T
The number of turns per unit length n can be calculated as:
We can rearrange the formula for the magnetic field to solve for the current I:
Now we can substitute the known values into the equation:
First, calculate the denominator:
Now substituting back into the equation for I:
The current in the solenoid is approximately 2.00A.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4×10−3Wb. The self-inductance of the solenoid is
View SolutionA long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4×10−3Wb. The self-inductance of the solenoid is
View Solution
Knowledge Check
The torque required to hold a small circular coil of 10 turns, area 1mm2 and carrying a current of (2144)A in the middle of a long solenoid of 103turns/m carrying a current of 2.5A, with its axis perpendicular to the axis of the solenoid is
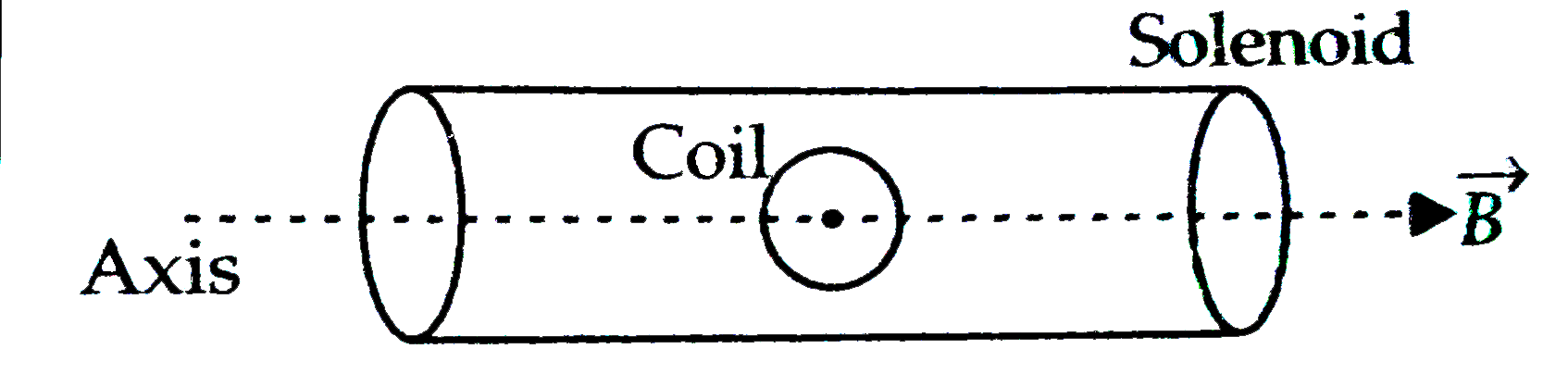 A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
A long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4×10−3Wb. The self-inductance of the solenoid is
View SolutionA long solenoid of 50 cm length having 100 turns carries a current of 2.5A. The magnetic field at centre of solenoid is:
View SolutionA closely wound solenoid of 800 turns and area of cross section 2⋅5×10−4m2 carries a current of 3⋅0A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
View SolutionA closely wound solenoid of 800 turns and area of cross section 2⋅5×10−4m2 carries a current of 3⋅0A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
View SolutionThe magnetic field B inside a long solenoid, carrying a current of 5.00 A, is (3.14×10−2) T. Find the number of turns per unit length of the solenoid.
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/m and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionA long solenoid having 200 turns per centimeter carries a current of 1.5A. At the center of the solenoid is placed a coil of 100 turns of cross-sectional area 3.14×10−4m2 having its axis parallel to the field produced by the solenoid. When the direction of current in teh solenoid is reversed within 0.05s, the induced emf in the coil is
View Solution
