A proton is projected with a speed of 3X106ms−1 horizontally from east to west. A uniform magnetic field →B of strength 2.0X10−3 T exists in the vertically upward direction(a) find the force on the proton just after it is projected. (b) what is the acceleration produced?
11.6×1011m/s2
17.4×1011m/s
5.8×1011m/s2
2.9×1011m/s2
The correct Answer is:c
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Finding the Force on the Proton
1. Identify the Given Values:
- Speed of the proton, v=3×106m/s
- Magnetic field strength, B=2.0×10−3T
- Charge of the proton, q=1.6×10−19C
- The direction of the velocity is from east to west (horizontally).
- The direction of the magnetic field is vertically upward.
2. Use the Formula for Magnetic Force:
The force F on a charged particle moving in a magnetic field is given by the equation:
F=q⋅(v×B)
Since the velocity v and the magnetic field B are perpendicular to each other, we can simplify this to:
F=q⋅v⋅B
3. Substitute the Values:
F=(1.6×10−19C)⋅(3×106m/s)⋅(2.0×10−3T)
4. Calculate the Force:
F=1.6×3×2.0×10−19×106×10−3
F=9.6×10−16N
Part (b): Finding the Acceleration Produced
1. Use Newton's Second Law:
The acceleration a produced on the proton can be calculated using Newton's second law:
a=Fm
where m is the mass of the proton.
2. Identify the Mass of the Proton:
The mass of the proton is given as:
m=1.67×10−27kg
3. Substitute the Values:
a=9.6×10−16N1.67×10−27kg
4. Calculate the Acceleration:
a=5.74×1011m/s2
Final Answers:
- (a) The force on the proton is 9.6×10−16N.
- (b) The acceleration produced is approximately 5.74×1011m/s2.
- Speed of the proton, v=3×106m/s
- Magnetic field strength, B=2.0×10−3T
- Charge of the proton, q=1.6×10−19C
- The direction of the velocity is from east to west (horizontally).
- The direction of the magnetic field is vertically upward.
The force F on a charged particle moving in a magnetic field is given by the equation:
F=q⋅(v×B)
Since the velocity v and the magnetic field B are perpendicular to each other, we can simplify this to:
F=q⋅v⋅B
F=(1.6×10−19C)⋅(3×106m/s)⋅(2.0×10−3T)
F=1.6×3×2.0×10−19×106×10−3
F=9.6×10−16N
The acceleration a produced on the proton can be calculated using Newton's second law:
a=Fm
where m is the mass of the proton.
The mass of the proton is given as:
m=1.67×10−27kg
a=9.6×10−16N1.67×10−27kg
a=5.74×1011m/s2
- (a) The force on the proton is 9.6×10−16N.
- (b) The acceleration produced is approximately 5.74×1011m/s2.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionAn electron is projectd horizontally with a kinetic energy of 10 keV. A magnetic feld of strength 1.0X10−7 T exists in the vertically upward direction. (a)will the electron deflect towards right or towards left of its motion? (b) calculate the sideways deflection of the electrion in travelling through 1m. make appropriate approximations.
View SolutionA charge of2.0μC moves with a speed of 2.0X106ms−1 along the positive x-axis. A magnetic field →B of strength (0.20→J+0.40→k)T exists in space. Find the magnetic force acting on the charge
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionA particle having a charge of 2.0X10−8C and a mass of 2.0X10−10g is projected with a speed of 2.0X103ms−1 in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
View SolutionTwo protons are projected simultaneously from a fixed point with the same velocity v into a region, magnetic there exists a uniform magnetic field. The magnetic field strength at B and it si perpendicular to the initial direction of v. One proton starts at time t=0 and another proton at t=πm2qB. The separation between them at time t=πmqB (where, m and q are the mass and charge of proton), will be approximately
View SolutionA proton of mass 1.67×10−27 kg charge 1.6×10−19C is projected in xy-plane with a speed of 2×106m/s at an angle of 60∘ to the X-axis. If a uniform magnetic field of 0.14 T is applies along the Y-axis, then the path of the proton is
View SolutionA body is projected horizontally from a height of 78.4 m with a velocity 10 ms−1 . Its velocity after 3 seconds is [g = 10 ms−2] (Take direction of projection on →i and vertically upward direction on j)
View SolutionA proton moves with a speed of 2.0×107ms−1 along the x -axis.It enters a region where there is a magnetic field of magnitude 1.5T directed at an angle of 30∘ to the x -axis and lying in the xy plane.The magnitude of the magnetic force on the proton is
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
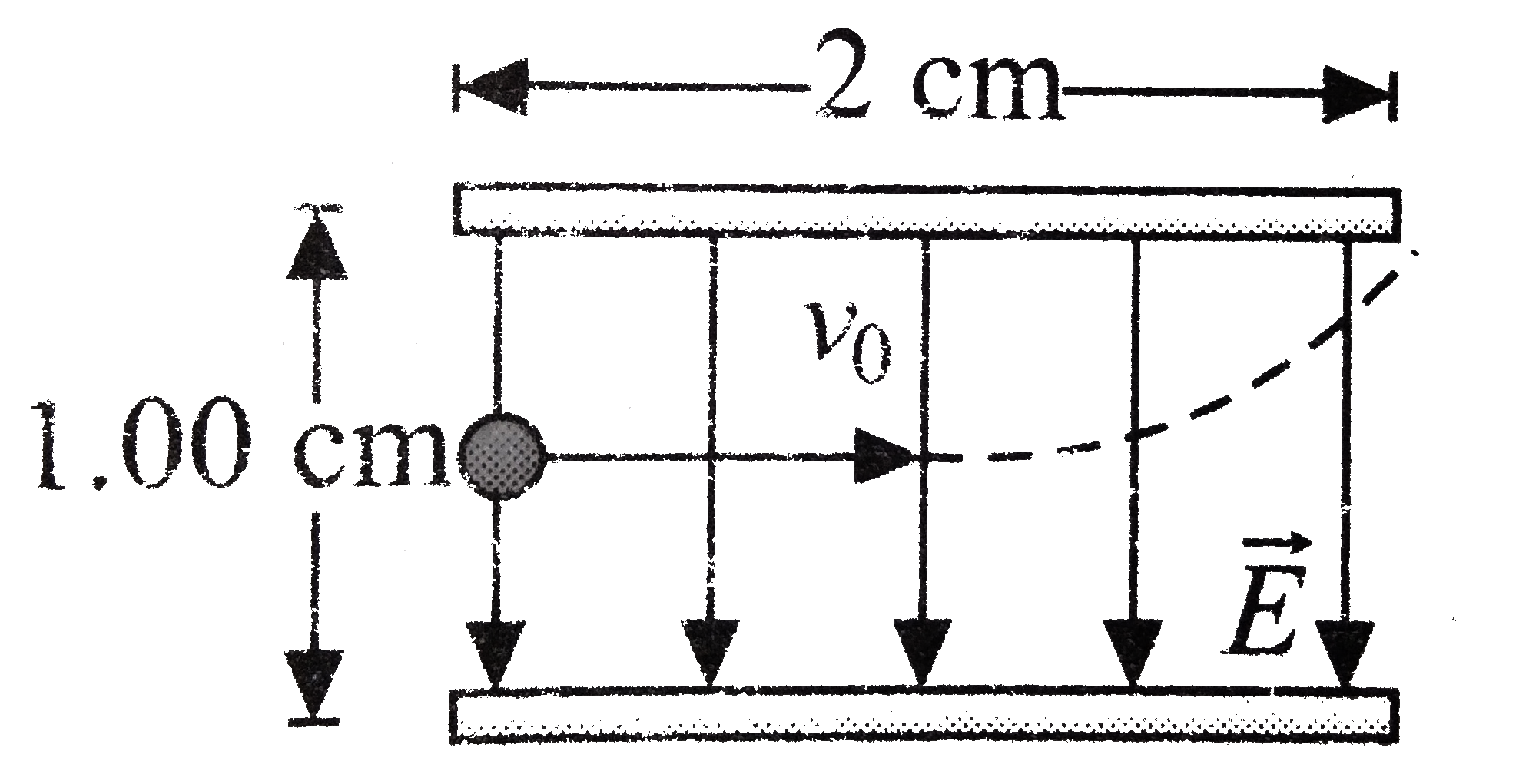
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View Solution
