Two ions having masses in the ratio 1:1 and charges 1:2 are projected into uniform magnetic field perpendicular to the field with speeds in th ratio 2:3. The ratio of the radius of circular paths along which the two particles move is
4:3
2:3
3:1
1:4
The correct Answer is:A
To solve the problem, we need to find the ratio of the radii of the circular paths of two ions projected into a uniform magnetic field. Let's denote the two ions as A and B.
Given Data:
1. Mass ratio: mAmB=11 (or mA=mB)
2. Charge ratio: QAQB=12 (or QB=2QA)
3. Velocity ratio: VAVB=23
1. Formula for Radius in a Magnetic Field:
The radius r of the circular path of a charged particle moving in a magnetic field is given by:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity,
- q is the charge,
- B is the magnetic field strength.
2. Calculate Radius for Ion A:
For ion A, the radius rA can be expressed as:
rA=mAVAQAB
3. Calculate Radius for Ion B:
For ion B, the radius rB can be expressed as:
rB=mBVBQBB
4. Finding the Ratio of Radii:
To find the ratio rArB:
rArB=mAVAQABmBVBQBB=mAVAQBmBVBQA
The B cancels out from the numerator and denominator.
5. Substituting Known Ratios:
Substitute the known ratios into the equation:
- Since mAmB=1, we have mA=mB (let's denote it as m).
- VAVB=23.
- Since QAQB=12, we have QB=2QA or QBQA=2.
Therefore,
rArB=mAmB⋅VAVB⋅QBQA=1⋅23⋅2
6. Calculating the Final Ratio:
rArB=23⋅2=43
Final Answer:
The ratio of the radius of circular paths along which the two particles move is:
rArB=43
1. Mass ratio: mAmB=11 (or mA=mB)
2. Charge ratio: QAQB=12 (or QB=2QA)
3. Velocity ratio: VAVB=23
The radius r of the circular path of a charged particle moving in a magnetic field is given by:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity,
- q is the charge,
- B is the magnetic field strength.
For ion A, the radius rA can be expressed as:
rA=mAVAQAB
For ion B, the radius rB can be expressed as:
rB=mBVBQBB
To find the ratio rArB:
rArB=mAVAQABmBVBQBB=mAVAQBmBVBQA
The B cancels out from the numerator and denominator.
Substitute the known ratios into the equation:
- Since mAmB=1, we have mA=mB (let's denote it as m).
- VAVB=23.
- Since QAQB=12, we have QB=2QA or QBQA=2.
rArB=mAmB⋅VAVB⋅QBQA=1⋅23⋅2
rArB=23⋅2=43
The ratio of the radius of circular paths along which the two particles move is:
rArB=43
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together75videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason20videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
Similar Questions
The path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
Two ions having masses in the ratio 1:1 and charges 1:2 are projected from same point into a uniform magnetic field with speed in the ratio 2:3 perpendicular to field. The ratio of radii of circle along which the two particles move is :View SolutionTwo charged particles having masses in the ratio 2:3 and charges in the ratio 1:2 are released from rest in a uniform electric field. After a time 1 minute their K.E. will be in the ratio of
View Solution
Knowledge Check
- Question 1 - Select One
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which :
Aits speed remains constant.Bits velocity remains constant.Cits momentum remains constant.Dits kinetic energy increases.
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which:
View SolutionA proton and an alpha particle enter the same magnetic field which is perpendicular to their velocity. If they have same kinetic energy then ratio of radii of their circular path is
View SolutionTwo electron beams having velocities in the ratio 1: 2 are subjected to the same transverse magnetic field. The ration of the radii is
View SolutionParticles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
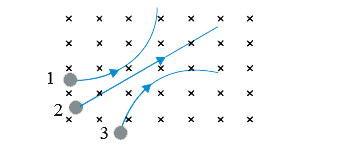 View Solution
View SolutionA charged particle enters a magnetic field at right angles to the field. The field exists for a length equal to 1.5 times the radius of circular path of particle. The particle will be deviated from its path by
View SolutionA proton and an α−particle, moving with the same velocity, enter a uniform magnetic field, acting normal to the plane of their motion. The ratio of the radii of the circular paths descirbed by the proton and α-particle is
View SolutionA proton an an α−particle, moving with the same velocity, enter a uniform magnetic field, acting normal to the plane of their motion. The ratio of the radii of the circular paths descirbed by the proton and α-particle is
View Solution

