H+,He+andO++ all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity . The masses of H+,He+andO2+ are 1aμ,4aμand16aμ respectively . Then
H+ ions will be deflected most
O2+ ions will be deflected least
He+ and O2+ ions will suffer same deflection
All ions will suffer the same deflection
The correct Answer is:A, C
To solve the problem, we need to analyze the motion of the ions H+, He+, and O2+ in a magnetic field. Given that they all have the same kinetic energy and are subjected to a uniform magnetic field that is perpendicular to their velocity, we can derive the radius of their circular paths.
1. Understanding Kinetic Energy:
The kinetic energy (KE) of a charged particle is given by the formula:
KE=12mv2
where m is the mass and v is the velocity of the particle.
2. Setting Up the Magnetic Force:
When a charged particle moves in a magnetic field, it experiences a magnetic force given by:
F=qvB
where q is the charge, v is the velocity, and B is the magnetic field strength.
3. Centripetal Force:
The magnetic force acts as the centripetal force that keeps the particle moving in a circular path:
F=mv2R
where R is the radius of the circular path.
4. Equating Forces:
Setting the magnetic force equal to the centripetal force, we have:
qvB=mv2R
Rearranging gives:
R=mvqB
5. Expressing Velocity in Terms of Kinetic Energy:
From the kinetic energy equation, we can express v:
v=√2KEm
Substituting this into the radius formula:
R=m√2KEmqB=√2m⋅KEqB
6. Calculating the Radius for Each Ion:
Since all ions have the same kinetic energy, we can analyze the radius for each ion:
- For H+ (mass = 1 amu, charge = +1):
RH=√2⋅1⋅KE1B=√2KEB2
- For He+ (mass = 4 amu, charge = +1):
RHe=√2⋅4⋅KE1B=2√2KEB2
- For O2+ (mass = 16 amu, charge = +2):
RO=√2⋅16⋅KE2B=2√2KEB2
7. Comparing the Radii:
- The radius for H+ is RH=√2KEB2
- The radius for He+ is RHe=2√2KEB2
- The radius for O2+ is also RO=2√2KEB2
8. Conclusion:
The radius of the path for H+ is the smallest, while both He+ and O2+ have the same larger radius. Thus, H+ will experience the maximum deflection, while He+ and O2+ will have the same deflection.
The kinetic energy (KE) of a charged particle is given by the formula:
KE=12mv2
where m is the mass and v is the velocity of the particle.
When a charged particle moves in a magnetic field, it experiences a magnetic force given by:
F=qvB
where q is the charge, v is the velocity, and B is the magnetic field strength.
The magnetic force acts as the centripetal force that keeps the particle moving in a circular path:
F=mv2R
where R is the radius of the circular path.
Setting the magnetic force equal to the centripetal force, we have:
qvB=mv2R
Rearranging gives:
R=mvqB
From the kinetic energy equation, we can express v:
v=√2KEm
Substituting this into the radius formula:
R=m√2KEmqB=√2m⋅KEqB
Since all ions have the same kinetic energy, we can analyze the radius for each ion:
- For H+ (mass = 1 amu, charge = +1):
RH=√2⋅1⋅KE1B=√2KEB2
- For He+ (mass = 4 amu, charge = +1):
RHe=√2⋅4⋅KE1B=2√2KEB2
- For O2+ (mass = 16 amu, charge = +2):
RO=√2⋅16⋅KE2B=2√2KEB2
- The radius for H+ is RH=√2KEB2
- The radius for He+ is RHe=2√2KEB2
- The radius for O2+ is also RO=2√2KEB2
The radius of the path for H+ is the smallest, while both He+ and O2+ have the same larger radius. Thus, H+ will experience the maximum deflection, while He+ and O2+ will have the same deflection.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
An electron and proton enter a uniform magnetic field perpendicularly. Both have same kinetic energy. Which of the following is true?
View SolutionAn electron and a proton are moving with the same kinetic energy along the same direction, When they pass through a uniform magnetic field perpendicular to the direction of their motion, they describe circular path of the same radius. Is this statement true or false?
View SolutionA proton and an electron are projected into a region of uniform magnetic field in a direction perpendicular to the field. If they have the same initial velocities then
View SolutionA proton and an alpha particle enter the same magnetic field which is perpendicular to their velocity. If they have same kinetic energy then ratio of radii of their circular path is
View SolutionCalculate the average energy required to extract a nucleon from the nucleus of an α - particle. the mass of 'alpha' -particle , proton and neutron are 4.00150 a.m.u 1.00728 a.m.u and 1.00867 amu respectively .
View SolutionHe32 and He31 nuclei have the same mass number. Do they have the same binding energy ?
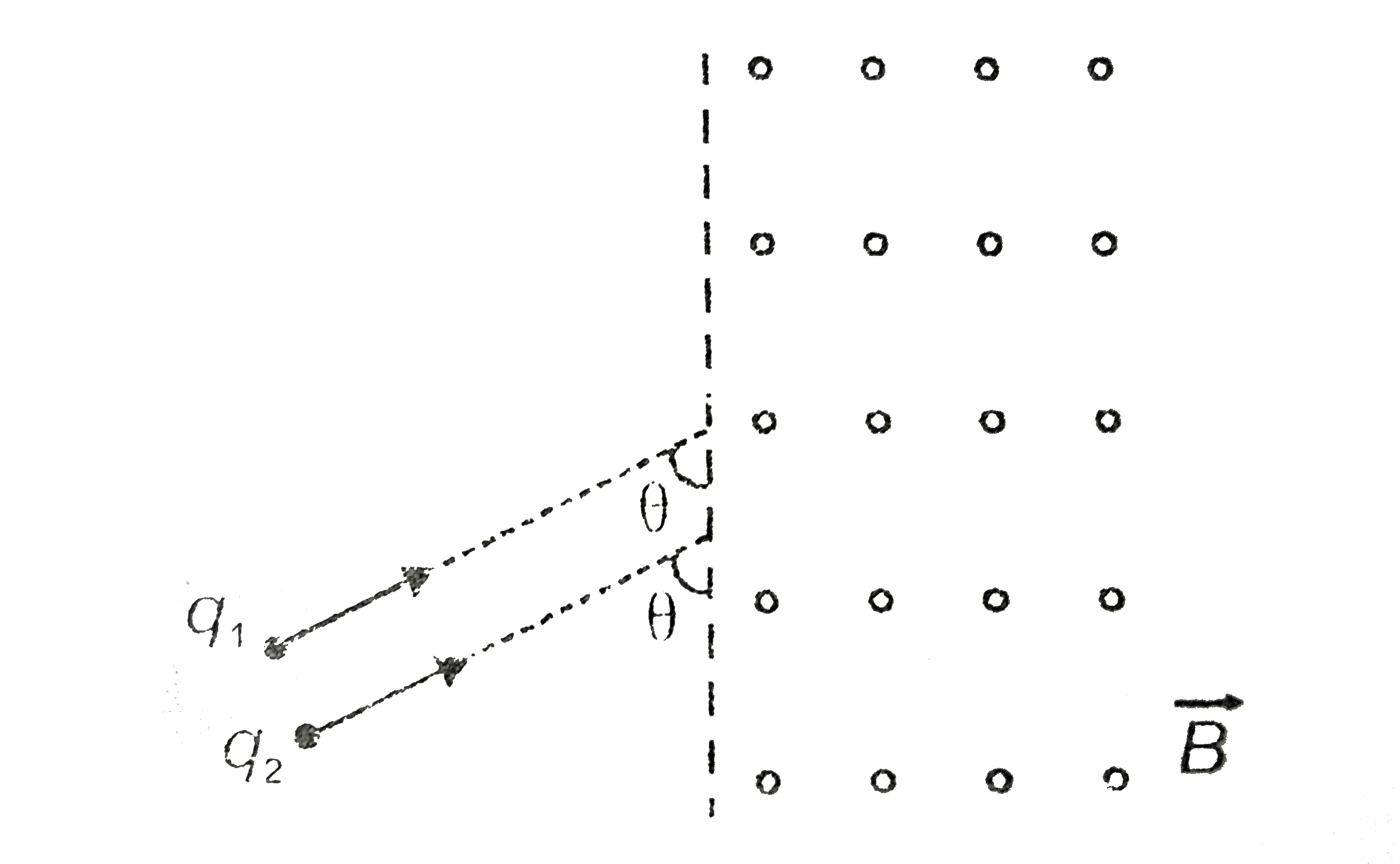
View SolutionTwo charges q1andq2 having same magneitude of charge are moving parallel to each other and they enter into a region of uniform magnetic field as shown. If they have same mass and the time spent by them in the magnetic field are t1andt2 respectively, then
View SolutionThe total kinetic energy of a mixture of 4 g of H2and4g of He at 300 K is
View SolutionA proton and an α-particle, accelerated through same potential difference, enter a region of uniform magnetic field with their velocities perpendicular to the field. Compare the radii of circular paths followed by them.
View SolutionAn electron and a proton enter region of uniform magnetic field in a direction at right angles to the field with the same kinetic energy. They describe circular paths of radius re and rp ?respectively. Then what will be the relation between re and rp?
View Solution
